Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Обобщенный закон Гука для случая объемного напряженного состояния
|
|
Рассмотрим элементарный объем линейно-упругого изотропного тела, находящийся в условиях объемного напряженного состояния, причем касательные напряжения на его гранях отсутствуют:
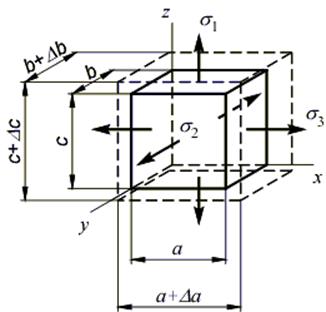
Таким образом, координатные грани элементарного объема являются главными площадками, координатные оси x, y, z – главными осями, нормальные напряжения, действующие на главных площадках – главными напряжениями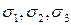 
и, соответственно, линейные относительные деформации в направлении главных осей – главными деформациями 
.
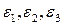По направлению осей x, y, z возникают абсолютные деформации D a, D b, D c.
Величина главной относительной деформации в направлении оси z: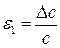 
.
Напряжение σ 1 приводит к увеличению D c, и по закону Гука
.
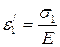Напряжения σ 2 и σ 3 работают на увеличение D a иD b и вызывают уменьшение D c, то есть, используя закон Гука и коэффициент поперечной деформации,
, 
.
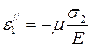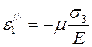Применяя принцип суперпозиции, находим
.
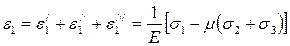Расписывая аналогичным образом главные деформаци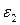и 
и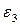 
, окончательно получим:
,
.
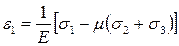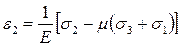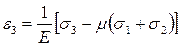
Полученные зависимости представляют собой обобщенный закон Гука в главной системе координат.
Проводя такие же рассуждения для элементарного объема, грани которого не являются главными площадками, получим обобщенный закон Гука в произвольной системе координат:
,
.
|
|
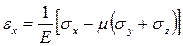