Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теории хрупкого разрушения

Первая теория прочности – теория наибольших нормальных напряжений (теория Галилея).

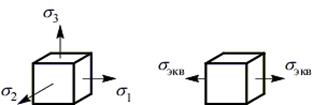
Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие нормальные напряжения

.

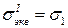Условие прочности при растяжении

.

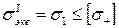Также можно использовать условие прочности для сжатия

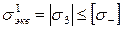. (2.7)

Данная теория нашла подтверждение только для весьма хрупких материалов (камень, бетон, кирпич). Ее основным недостатком является неучет двух главных напряжений.

Вторая теория прочности – теория наибольших линейных деформаций (теория Мариотта).

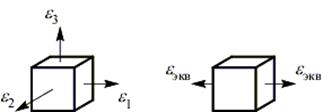
Критерий равнопрочности: напряженных состояния равнопрочны по хрупкому разрушению, если у них равны наибольшие линейные относительные деформации

.

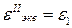Согласно закону Гука, при одноосном напряженном состоянии

.

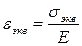Наибольшую линейную относительную деформацию при произвольном напряженном состоянии запишем, используя обобщенный закон Гука:

.

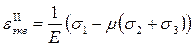Приравнивая правые части, получим эквивалентное напряжение по второй теории

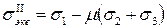. (2.8)

Вторая теория применима только для хрупких материалов, в том числе для хрупких металлов.