Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовая задача с решением. Задана реализация стационарного эргодического случайного процесса х(t) при некотором времени наблюдения этого процесса t
|
|
Задана реализация стационарного эргодического случайного процесса х (t) при некотором времени наблюдения этого процесса T. Определить оценки математического ожидания процесса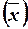 
, корреляционной функции процесса 
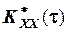, а также его дисперсии (
).
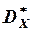Цель предложенного задания – закрепить принцип решения одной из задач статистики случайных процессов: определения характеристик эргодического процесса по одной его реализации, регистрируемой в течение достаточно длительного времени. Xарактеристики такого процесса, как правило, определяются в темпе самого процесса с помощью специальной аппаратуры, реализующей алгоритмы, рассмотренные ниже. В задании при аналитическом представлении процесса предполагается найти характеристики этого процесса также аналитически.
Очевидно, что эти характеристики будут зависеть от времени наблюдения процесса: чем больше это время, тем с большей точностью они определяются.
Несмещенная и состоятельная оценка математического ожидания эргодического процесса определяется как
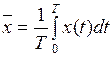. (5.1)
Несмещенная и состоятельная оценка корреляционной функции эргодического процесса при его единственной реализации x (t), будет
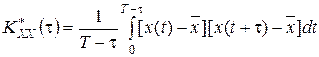(5.2)
Аппаратные или программные средства при регистрации эргодического процесса реализуют для определения его характеристик выражения (5.1), (5.2).
1.1. x (t)=sinw t, T =6p/w.
Решение
,
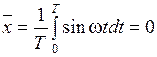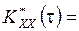
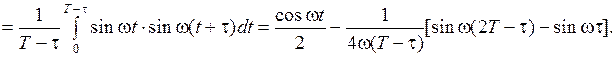При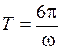 
, 
.
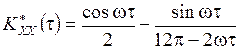Оценка дисперсии в последнем случае будет: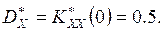 
 |
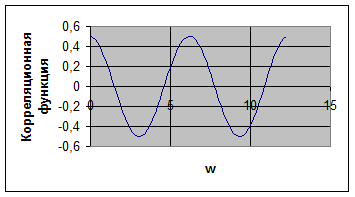Рис.5.1
На рисунке 5.1 приведена зависимость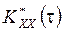 
от параметра w=wt. Из рисунка видно, что зависимость носит колебательный характер с периодом w=2p.
1.2 x (t)=exp(- t 2/2)cos t, T =3 ч.
Решение
В рассматриваемом примере интегралы (5.1) и (5.2) не определяются аналитически и могут быть вычислены лишь с помощью любого численного метода. При заданных параметрах процесса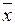 
=0.254 ч., зависимость 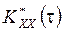приведена на рис.5.2.
 |
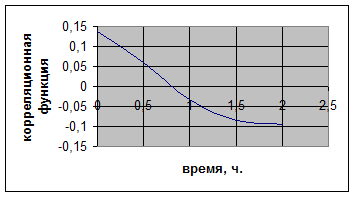Рис.5.2
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО РАЗДЕЛУ 5
При заданных стационарном эргодическом процессе X (t) и времени его наблюдения Т определить оценки его математического ожидания 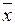, корреляционной функции 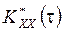и дисперсии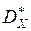 
. Построить зависимость 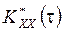при заданном времени наблюдения процесса. При построении диапазон значений t принимать несколько меньшим времени Т.
| Номер варианта | X(t) | Параметры X(t) | T |
| a + sinw t | a =1 | w T =3p | |
| cosw t | - | w T =6p | |
| a + cosw t | a =1 | w T =6p | |
| sin(w t + p/4) | - | w T =6p | |
| cos(w t + p/4) | - | w T =6p | |
| exp(-a t)´ sinb t | a=b=1 1/ч | 4 ч | |
| a + exp(-a t)´ sinb t | a =1; a=b=1 1/ч | 4 ч | |
| exp(-a t)´ cosb t | a=b=1 1/ч | 4 ч | |
| a + exp(-at)´ cosbt | a =1; a=b=1 1/ч | 4 ч | |
| exp(-a t)´ sin(b t +p/4) | a=b=1 1/ч | 3 ч | |
| exp(-a t)´ cos(b t +p/4) | a=b=1 1/ч | 3 ч | |
| exp(-a t 2)´ sinb t | a=1 1/ч2; b=1 1/ч | 2 ч | |
| exp(-a t 2)´ sin(b t + p/4) | a=1 1/ч2; b=1 1/ч | 2 ч | |
| exp(-a t 2)´ cos(b t + p/4) | a=1 1/ч2; b=1 1/ч | 2 ч | |
| exp(-a t)´ t | a=1 1/ч | 4 ч | |
| exp(-a t)´ (t +1) | a=1 1/ч | 4 ч | |
| exp(-a t 2)´ t | a=1 1/ч2 | 2 ч | |
| exp(-a t 2)´ (t +1) | a=1 1/ч2 | 2 ч |
Литература
1. Кадомская К.П., Костенко М.В., Левинштейн М.Л. Теория вероятностей и её приложения к задачам электроэнергетики. С.Пб.: Наука.-1992.-376 с.
|
|