
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовая задача с решением. Найти математические ожидания числа выбросов стационарного нормального случайного процесса за заданный уровень с в течение времени т (m[n(c;t)]) и времени
|
|
Найти математические ожидания числа выбросов стационарного нормального случайного процесса за заданный уровень с в течение времени Т (M [ N (c; T) ] ) и времени пребывания процесса X (t ) за время Т выше этого уровня (M [ Tc ]). Заданы математическое ожидание и корреляционная функция стационарного процесса X (t): M [ X (t)]=0, 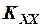 (t)=
(t)= 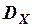
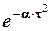 ; c =1;
; c =1; 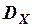 = 1; a=2 1/ч2; Т =10 ч.
= 1; a=2 1/ч2; Т =10 ч.
Решение
Математическое ожидание числа выбросов стационарного случайного процесса за время Т выше уровня сопределяется по выражению:
M [ N (c; T)]= 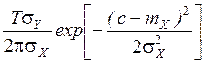 , (4.1)
, (4.1)
где s Y – среднеквадратическое отклонение случайного процесса Y = 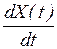 .
.
Дисперсия D [ Y ]= KYY (0), а KYY (t)= - 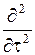 KXX (t).
KXX (t).
В рассматриваемом примере
KYY (t)= 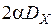 [
[ 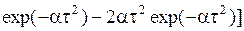 . (4.2)
. (4.2)
Из (4.2) следует, что K YY ( 0 )= DY = 2a DX. При подстановке числовых значений a и DX DУ= 4 и s Y =2.
Подставив в (4.1) s Y и остальные параметры, получим M [ N (c; T)]= M [ N (1; 10)]=1.93 ч.
Математическое ожидание времени нахождения в течение интервала Т нормального случайного процесса X (t) выше уровня с определяется как
M [ Tc ]= T × 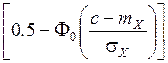 , (4.3)
, (4.3)
где 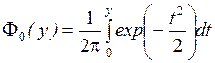 — функция Лапласа (интеграл вероятности).
— функция Лапласа (интеграл вероятности).
Следует отметить, что при решении задачи о выбросах, связанной с определением корреляционной функции процесса Y (t)= 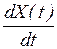 , производная корреляционной функция процесса X(t) должна быть непрерывной.
, производная корреляционной функция процесса X(t) должна быть непрерывной.
В табл. 4.1 приведены выражения для KXX (t), принятые в вариантах задания 4.
Таблица 4.1
| Номер KXX (t) | KXX (t) |
| DX exp(-at2)cosbt | |
| DX exp(-g|t|)(1+g|t|) | |
DX exp(-g|t|)(cosbt+ 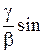 b|t|) b|t|)
|
Варианты заданий приведены в табл. 4.2.
Таблица 4.2
| Номер варианта | НомерKXX(t) | c | mX | sX | T, ч. | a 1/час2 | g 1/час | b 1/час |
| - | 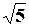
| |||||||
| - | 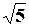
| |||||||
| - | 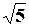
| |||||||
| - | ||||||||
| - | ||||||||
| - | ||||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | - | |||||||
| - | 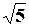
| |||||||
| - | 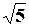
| |||||||
| - | 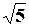
| |||||||
| - | ||||||||
| - | ||||||||
| - |
|
|
