Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовая задача с решением. Найти оптимальную передаточную функцию линейной системы, представляющую собой фильтр с упреждением на время t0
|
|
Найти оптимальную передаточную функцию линейной системы, представляющую собой фильтр с упреждением на время t 0. На вход системы поступают полезный сигнал и помеха, характеризуемые корреляционными функциями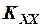 
(t)=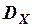 
e -aô tô 
= 
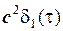, соответственно.
Решение уравнения Винера-Хопфа позволяет получить следующее выражение для оптимальной передаточной функции линейной системы, обеспечивающей минимум дисперсии ошибки на выходе системы (предполагается, что система астатическая, т.е. M [ U ]= 0):
H (p)=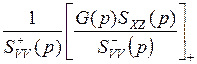 
, (3.13)
где V (t)= X (t) + U (t) – суммарный сигнал на входе линейной системы,
SVV (p)=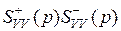 
– факторизация спектральной плотности суммарного сигнала на входе линейной системы,
Z (t) – желаемый сигнал на выходе линейной системы,
SXZ (p) – взаимная спектральная плотность между случайными процессами на входе X (t) и выходе Z (t) системы.
Обозначим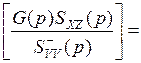 
Ф(p) и представим Ф(р) в виде:
Ф(р)=Ф+(р) + Ф-(р), (3.14)
где Ф+(р) и Ф-(р) – составляющие, содержащие левые и правые полюса Ф(р) соответственно. Эти составляющие при условии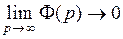 
могут быть определены с помощью выражений:
Ф+(р) = -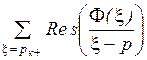 
, (3.15)
Ф-(р) = -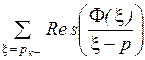 
, (3.16)
где рк+ и рк- - левые и правые полюса Ф(р), соответственно.
В рассматриваемом примере оптимизации структуры фильтра помехи c упреждением Z (t)= X (t + t 0), G (p)=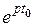 
, SVX (p)= SXX (p) и выражение (3.13) переписывается в виде
H (p)=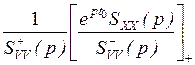 
, (3.17)
где SVV (p)= SXX (p)+ SUU (p)=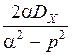 
+ c 2= 
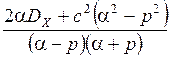. (3.18)
Осуществляя факторизацию (3.18), получаем
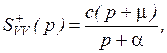
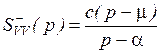, (3.19)
где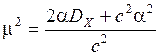 
. (3.20)
Следовательно, в рассматриваемом примере
Ф(р)=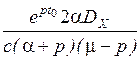 
. (3.21)
Выделяя составляющую Ф+(р), будем иметь
Ф+(р)=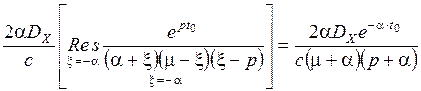 
. (3.22)
Подставив (3.19) и (3.22) в (3.17), получим
H(p)=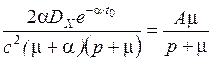 
, (3.23)
где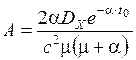 
.
 |
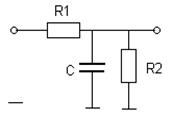Из выражения (3.23) видно, что оптимальным линейным звеном, осуществляющим задачу фильтрации сигнала от помехи с упреждением, является интегрирующее звено. Если ориентироваться на пассивную электрическую схему, то линейная система может иметь вид, показанный на рис.3.4
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Рис.3.4
В этой схеме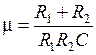 
, 
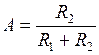. (3.24)
Величины m и А зависят от характеристик корреляционных функций полезного сигнала и помехи, которые предполагаются известными. Следовательно, на основании двух выражений (3.24) должны быть определены три параметра схемы рис.3.4. Поэтому один из этих параметров может быть принят произвольно, исходя из каких-либо соображений; два других же параметра определятся из выражений (3.24).
|
|