
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения по разделам 1 и 2
|
|
Задания 1 и 2
Задача 1. Во всех вариантах найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса X (t) при заданных числовых характеристиках составляющих этого процесса.
| Номер варианта | X (t) | Числовые характеристики составляющих X (t) |
| Y cosw t + Z sinw t + 5 t | M [ Y ]=1; M [ Z ]=0.2; D [ Y ]=0.1; D [ Z ] = 0.004; KYZ = 0 | |
| Y sinw t | M [ Y ] = 1; D [ Y ] = 0.2 | |
| Yt – Z t 2 | M [ Y ] = 3; M [ Z ] = 0.5; D [ Y ]=1; D [ Z ] = 0.5; KYZ = 0 | |
| 2 Y sinwt + 3 Zt 2 + 5 | M [ Y ]= 1; M [ Z ] = 2; D [ Y ]= 0.1; D [ Z ] = 0.05; KYZ = 0 | |
| t –3cos t + Y (t + cos t)+ Z cos2 t | M [ Y ]= M [ Z ]=0; D [ Y] = 1; D [ Z ] = 2; KYZ = 0 | |
| cos tY (t) + sinw t | 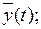 KYY (t 1, t 2) KYY (t 1, t 2)
| |
| Y (t) + t cos t | 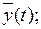 KYY (t 1, t 2) KYY (t 1, t 2)
| |
Y 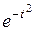 
| M [ Y ] = 2; D [ Y ] = 0.01 | |
Y cosw t + 5 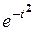
| M [ Y ] = 0; D [ Y ] = 1 | |
| Ye-t + sinw t | M [ Y ] = D [ Y ] = 1 | |
| Ye-t + Zet | M [ Y ]= 2; M [ Z ]=-2; D [ Y ] = D [ Z ] = 1; KYZ = 0 | |
| Y sinw t + 4 e-t | M [ Y ] = 2; D [ Y ] = 0.1 | |
| Yt + Ze-t + V sinw t | M [ Y ]= M [ Z ]= M [ V ]= D [ Y ]= D [ Z ]= D [ V ]=1; KYZ = KYV = KZV = 0 | |
| Y sinw t + Z cosw t + Ve-t | M [ Y ]=2; M [ Z ]= M [ V ]=1; D [ Y ]= D [ V ]=0.1; D [ Z ]=0.05; KYZ = KYV=KZV =0 | |
| Yte-t + Z | M [ Y ]=2; M [ Z ]=1; D [ Y ]=0.2; D [ Z ]=0.1; KYZ = 0 | |
| 5 Ye-t + sinw t | M [ Y ]=2; D [ Y ]=4 | |
| Ye-t + Z sinw t | M [ Y ]= D [ Y ]=1; M [ Z ]=2; D [ Z ]=1; KYZ = 0 | |
| Ye-t + Z cosw t + 3sinw t | M [ Y ]= M [ Z ]=2; D [ Y ]=2; D [ Z ]=1; KYZ = 0 |
Задача 2. Используя понятие спектральной плотности, найти корреляционную функцию и дисперсию стационарного случайного процесса на выходе линейной системы при известной корреляционной функции стационарного эргодического процесса на её входе: KXX (t) = DXe -aô tô .
Варианты линейных систем
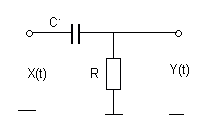 | 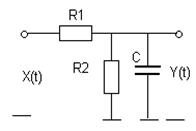 | ||
№ 1 № 2
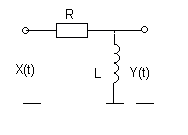 |
№ 3 № 4
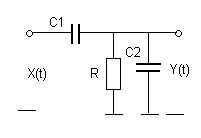 | 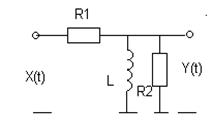 | ||
№ 5 № 6
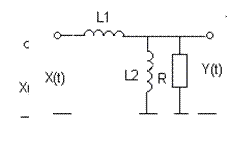 | 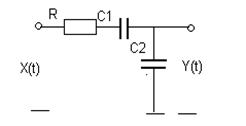 | ||
№ 7 № 8
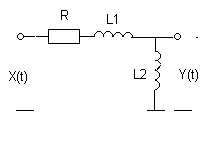 | 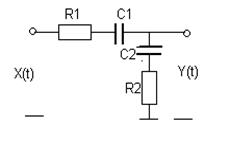 | ||
№ 9 № 10
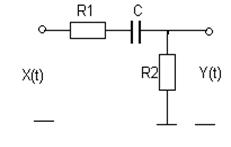 | 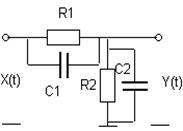 | ||
№ 11 № 12
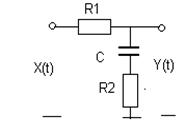 |
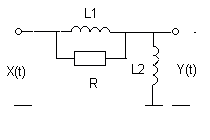 |
№ 13 № 14
№ 15 № 16
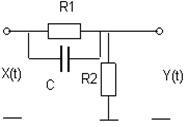 | 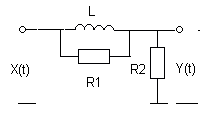 | ||
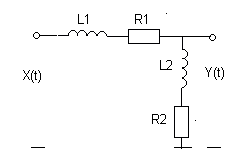 |
№ 17 № 18
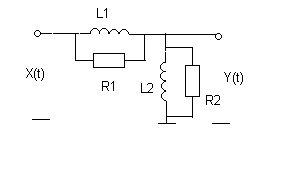 |
|
|
