
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовая задача с решением
|
|
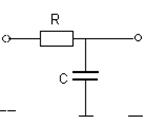 |
Найти значение постоянной времени линейной системы, отвечающее минимуму дисперсии ошибки на выходе этой системы, являющейся фильтром. Рассмотрим в качестве линейной системы простейшее интегрирующее звено (рис. 3.1).
Рис. 3.1
Решение
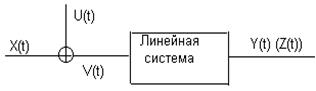 |
Ошибка на выходе системы обусловлена тем, что на вход системы поступает не только полезный случайный процесс X (t), но и помеха, также представляющая собой случайный процесс U (t) (рис.3.2).
Рис. 3.2
Таким образом, на вход системы поступает суммарный сигнал
V (t) = X (t) + U (t). (3.1)
На выходе системы вместо желаемого сигнала Z(t) возникает сигнал Y(t). Таким образом, ошибка на выходе системы определяется как
E (t) = Z (t) – Y (t). (3.2)
Операторное изображение желаемого сигнала на выходе системы связано с операторным изображением полезного сигнала на её входе с помощью выражения
Z (p) = X (p)× G(p), (3.3)
где G (p) – передаточная функция системы при условии отсутствии помехи.
Операторное изображение истинного сигнала на выходе системы связано с операторным изображением суммарного сигнала на её входе с помощью передаточной функции H (p):
Y (p) = V (p)× H (p). (3.4)
Операторное изображение ошибки с учетом приведенных выше выражений определится как
E (p) = X (p)[ G (p)- H (p)] – U (p) H (p). (3.5)
При решении задачи фильтрации помехи Z(t)=X(t) и G(t)=1. Как правило, систематическая ошибка на выходе системы отсутствует (такая система называется астатической). Поэтому критерием оптимальности системы может, в частности, служить минимум дисперсии ошибки на её выходе. Для определения дисперсии ошибки предварительно целесообразно определить корреляционную функцию cтационарного процесса на выходе (KYY (0)= DY). При заданных корреляционных функциях полезного случайного процесса и помехи на входе и заданной структуре передаточной функции линейной системы DY будет зависеть лишь от параметров этой системы, которые и надлежит определять, исходя из требования минимизации ошибки на выходе системы.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
При решении этой задачи целесообразно воспользоваться понятием спектральной плотности случайного процесса, которая в рассматриваемом случае фильтрации помехи определится как
SEE (p)= SXX (p)(1- H (p))(1- H (- p)) + SUU (p) H (p) H (- p). (3.6)
Затем с помощью обратного двустороннего преобразования Лапласа [выражения (2.3) и (2.4)] определяется KEE (t) и, наконец, DE.
В рассматриваемом примере примем, что на вход системы рис. 3.1 поступает полезный стационарный случайный процесс, характеризующийся корреляционной функцией KXX (t)= DXe -aô tô и помеха, представляющая собой белый шум – KUU (t)= 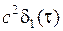 , где d1(t) – импульсная функция первого рода (функция Дирака). Спектральные плотности этих процессов запишутся в виде:
, где d1(t) – импульсная функция первого рода (функция Дирака). Спектральные плотности этих процессов запишутся в виде:
SXX (p)= 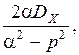 SUU (p)= c 2. (3.7)
SUU (p)= c 2. (3.7)
Передаточная функция интегрирующей линейной системы (рис.3.1) будет
H (p)=d/(p +d), где d=1/ RC. (3.8)
Спектральная плотность ошибки в соответствии с выражением (3.6) определится как
SEE (p)=- 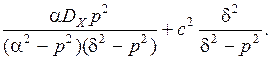 (3.9)
(3.9)
Переходя в (3.9) к оригиналу при t> 0 [выражение (2.3)], получим
KEE (t)= 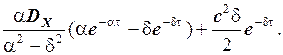
 (3.10)
(3.10)
Полагая в (3.10) t=0, получим
DE = 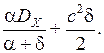 (3.11)
(3.11)
При заданных параметрах корреляционных функций KXX(t) и KUU(t) величина дисперсии DE зависит лишь от параметра линейной системы d=1/Т (Т=RC – постоянная времени схемы рис. 3.1). Зависимость DE=f(d) при DX=2, a =1 1/с, с=0.5 в рассматриваемом случае приведена на рис.3.3. Из рисунка следует, что при некотором значении d наблюдается минимальная дисперсия ошибки, т.е. при заданных характеристиках полезного сигнала и помехи на входе системы последняя при этом значении T=1/d является оптимальной.

Рис.3.3
Значение d, отвечающее DEmin, можно получить и аналитически, взяв производную по d от выражения (3.11) и приравняв её нулю. Выражение для dопт при этом имеет вид
dопт 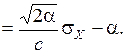
 (3.12)
(3.12)
В рассматриваемом примере dопт=3 1/с и соответственно Т опт=1/3 с.
|
|
