Найти математическое ожидание, корреляционную функцию и дисперсию процесса

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Х (t) = sin t× Y (t) + cos t,

где Y (t) – случайный процесс, характеризуемый M [ Y (t)] и K_YY (t ₁, t ₂),

cos t – неслучайный процесс.

Решение

Математическое ожидание процесса X (t) определится как:

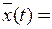sin t× 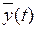+ cos t.

Корреляционная функция процесса X (t) запишется в виде

K_XX (t) = sin t ₁× sin t₂ × K_YY (t ₁, t ₂),

(корреляционная функция неслучайного процесса равна нулю).

Соответственно дисперсия случайного процесса X (t) будет

D_X (t) = sin² t× (t).

ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ПРИ ИСПОЛЬЗОВАНИИ ПОНЯТИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ

ТИПОВАЯ ЗАДАЧА С РЕШЕНИЕМ

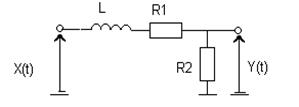Используя понятие спектральной плотности, найти дисперсию процесса на выходе линейной системы (рис.2.1) при воздействии на её входе стационарного процесса X (t), характеризуемого корреляционной функцией 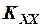(t) = 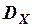e ^-^a^ï^t^ï.

Рис. 2.1

⇐ Предыдущая 1 234 5 6 7 8 9 10 Следующая ⇒