Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса
|
|
X (t) = Y sin 2 w t + Z cosw t,
где Y и Z – случайные величины, характеризуемые следующими числовыми характеристиками: m Y = 2, mZ = 1, DY = 0.1, DZ = 0.05,
корреляционный момент между случайными величинами Y и Z
K YZ = 0.
Решение
В рассматриваемом случайном процессе множители sin2w t и cosw t не являются случайными величинами. Поэтому при определении математического ожидания процесса Х (t) они выносятся за знак математического ожидания случайных величин Y и Z. Математическое же ожидание суммы равно сумме математических ожиданий составляющих случайного процесса:
M [ X (t)] =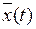 
= sin2w t × M [ Y ]+ cosw t × M [ Z ].
Подставляя в последнее выражение числовые значения M[ Y ] и M [ Z ], получим
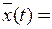2sin2w t + cosw t.
Поскольку случайные величины Y и Z некоррелированы, корреляционная функция процесса X (t) равна сумме корреляционных функций его составляющих. При этом коэффициенты (неслучайные процессы) выносятся за знак корреляционных функций случайных величин Y и Z в виде произведения неслучайных процессов в двух сечениях по времени t 1 и t 2. Учитывая также, что
К YY (t 1, t 2)=D Y и K ZZ (t 1, t 2)=D Z, будем иметь
KXX (t 1, t 2)=sin2w t 1× sin2w t 2 × DY + cosw t 1× cosw t 2× DZ.
Подставляя числовые значения для DY и DZ, получим
KXX (t 1, t 2)=0.1sin2w t 1× sin2w t 2 + 0.05cosw t 1× cosw t 2.
Дисперсия случайного процесса X (t) определится как DX (t)= KXX (t 1, t 2) при t 1= t 2= t:
DX (t) = 0.1sin22w t + 0.05cos2w t.
|
|