Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задачи для самостоятельного решения по продразделу 3. 1
|
|
Задание 3
Во всех вариантах задания найти значение постоянной времени линейной динамической системы, отвечающее минимуму дисперсии ошибки на выходе системы. Корреляционная функция полезного сигнала на входе системы описывается выражением KXX (t)= DXe -a÷ t÷ (DX =1, величина a определена в вариантах задания).В вариантах заданияприняты два вида корреляционной функции помехи: функция того же вида, что и функция полезного сигнала: KUU (t)= DUe -g÷ t÷ (DU =2, g=2 1/c; в вариантах задания обозначена как функция № 1), и корреляционная функция случайного процесса вида " белый шум" KUU (t)=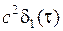 
(с =0.5; в вариантах задания обозначена как функция № 2).
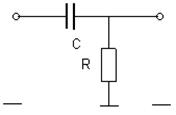
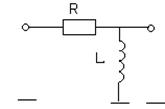
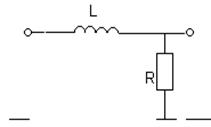
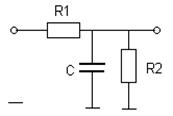
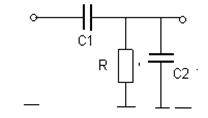
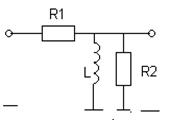
В заданиях рассматривается 8 пассивных линейных динамических систем, процессы в которых описываются линейными дифференциальными уравнениями первого порядка.
Варианты линейных систем
 |  | ||
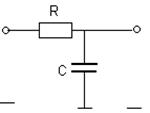№1. № 2.
 |  | ||
№ 3 № 4
 |  | ||
№ 5 № 6
 |  | ||
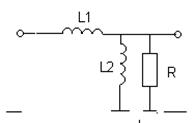№ 7 № 8
| Номер варианта | a, 1/с | Номер KUU (t) | Номер схемы |
| 0.25 | |||
| 0.25 | |||
| 0.50 | |||
| 0.50 | |||
| Номер варианта | a, 1/с | Номер KUU (t) | Номер схемы |
| 0.50 | |||
| 1.00 | |||
| 1.00 | |||
| 1.00 | |||
| 0.75 | |||
| 0.75 | |||
| 0.75 | |||
| 0.25 | |||
| 0.25 | |||
| 1.00 | |||
| 0.75 | |||
| 0.75 | |||
| 0.75 | |||
| 1.50 |
3.2.ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОЙ СИСТЕМЫ ПРИ НЕЗАДАННОЙ ЕЁ СТРУКТУРЕ. УРАВНЕНИЕ ВИНЕРА-ХОПФА
|
|