
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые характеристики случайных векторов
|
|
Рассмотрим вначале двумерный 
 .
.
Прежде, чем приводить соответствующие определения, сформулируем обобщение основной теоремы о математическом ожидании (ОТМО) на случай функции двух переменных 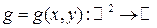 .
.
Теорема (обобщение ОТМО на двумерный случай).
Пусть  - некоторый
- некоторый  , ЗР которого известен,
, ЗР которого известен, 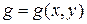 - неслучайная функция, область определения которой содержит множество возможных значений
- неслучайная функция, область определения которой содержит множество возможных значений 
 ,
, 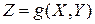 - СВ, являющаяся функцией двух случайных аргументов.
- СВ, являющаяся функцией двух случайных аргументов.
1. Если  -
- 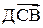 , принимающий значения
, принимающий значения 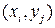 с вероятностями
с вероятностями 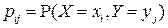 , и ряд
, и ряд 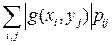 сходится, то у СВ
сходится, то у СВ 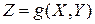 существует МО и
существует МО и
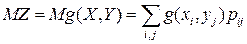 .
.
2. Если  -
- 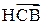 с ПВ
с ПВ 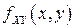 и несобственный интеграл
и несобственный интеграл 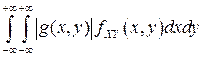 сходится, то у СВ
сходится, то у СВ 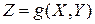 существует МО и
существует МО и
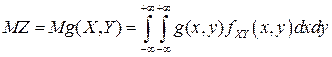 .
.
Заметим, что приведенная теорема очевидным образом обобщается и на случай функции 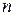 переменных
переменных 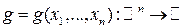 .
.
Теперь перейдем к рассмотрению числовых характеристик (ЧХ).
Основными ЧХ двумерного 
 являются:
являются:
· математическое ожидание 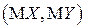 - вектор, координатами которого являются математические ожидания СВ
- вектор, координатами которого являются математические ожидания СВ  и
и  (характеризует координаты средней точки, около которой группируются другие значения вектора
(характеризует координаты средней точки, около которой группируются другие значения вектора  );
);
· дисперсия 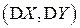 - вектор, координатами которого являются дисперсии СВ
- вектор, координатами которого являются дисперсии СВ  и
и  (характеризует степень разброса (рассеивания) значений вектора
(характеризует степень разброса (рассеивания) значений вектора  около его среднего значения
около его среднего значения 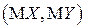 );
);
· корреляционный момент  СВ
СВ  и
и  - МО произведения отклонений этих СВ относительно их МО:
- МО произведения отклонений этих СВ относительно их МО:
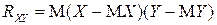 . (3.17)
. (3.17)
Как будет показано далее, корреляционный момент  характеризует степень линейной зависимости между СВ
характеризует степень линейной зависимости между СВ  и
и  .
.
Для корреляционного момента  справедливо также следующее выражение:
справедливо также следующее выражение:
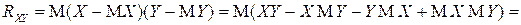
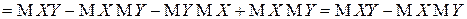 .
.
Таким образом, наряду с (3.12),
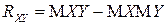 . (3.18)
. (3.18)
Корреляционный момент  обладает следующими двумя очевидными свойствами:
обладает следующими двумя очевидными свойствами:
1. 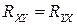 ;
;
2. 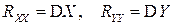 .
.
Благодаря этим свойствам, вектор дисперсий 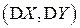 можно не рассматривать как самостоятельную ЧХ, а использовать объединенную характеристику – корреляционную матрицу, элементами которой являются всевозможные корреляционные моменты:
можно не рассматривать как самостоятельную ЧХ, а использовать объединенную характеристику – корреляционную матрицу, элементами которой являются всевозможные корреляционные моменты:
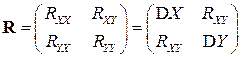 .
.
Таким образом, можно считать, что 
 имеет две основные ЧХ:
имеет две основные ЧХ:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
· математическое ожидание 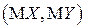 ;
;
· корреляционную матрицу 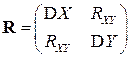 .
.
Математические ожидания 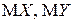 и дисперсии
и дисперсии 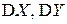 координат
координат 
 могут быть вычислены как по двумерному ЗР с помощью обобщения ОТМО, так и по обычным формулам через одномерные ЗР СВ
могут быть вычислены как по двумерному ЗР с помощью обобщения ОТМО, так и по обычным формулам через одномерные ЗР СВ  и
и  .
.
Так, если  -
- 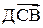 , то при
, то при 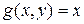 имеем:
имеем:
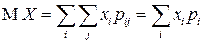 , где
, где 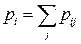 ,
,
а при 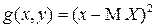 или
или 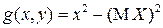
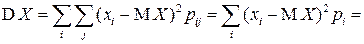
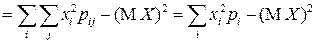 , где
, где 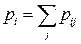 .
.
Аналогичны выражения для 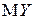 и
и 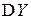 (написать самостоятельно).
(написать самостоятельно).
Корреляционный момент  вычисляется с помощью обобщения ОТМО, когда функция
вычисляется с помощью обобщения ОТМО, когда функция 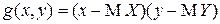 или
или 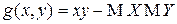 и только по двумерному закону распределения:
и только по двумерному закону распределения:
если  -
- 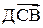 , то
, то
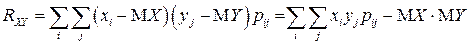 ;
;
если  -
- 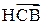 , то
, то
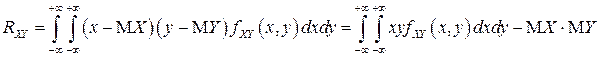 .
.
|
|
