Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Независимость случайных величин
|
|
Известно, что события А и В являются независимыми, если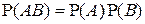 
. Аналогично определяется и независимость СВ 
и 
, только вместо событий А и В следует использовать события, связанные с этими СВ.
Определение. СВ и называются независимыми, если для любых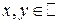 
имеет место равенство:
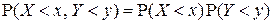
или, что эквивалентно, в терминах ФР
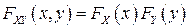. (3.9)
Если при каких-либо 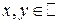равенство (3.9) не выполняется, то говорят, что СВ и являются зависимыми.
Таким образом, независимость СВ означает, что их совместная ФР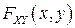 
равна произведению одномерных ФР 
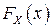и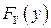 
, или, как еще говорят, двумерная ФР 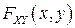факторизуется.
Отметим, что установить, являются зависимыми или независимыми СВ и , можно только по определению (3.9) и только, зная их совместный (двумерный) ЗР (никакая вероятностная интуиция при этом не работает).
Установим условия независимости СВ в дискретном и непрерывном случаях.
Лемма 1.
Пусть 
- 
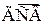, принимающий значения 
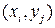с вероятностями 
, 
; 
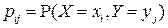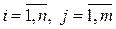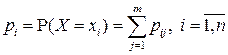, - вероятности возможных значений СВ , 
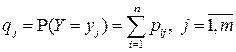- вероятности возможных значений СВ .
ДСВ и являются независимыми тогда и только тогда, когда при всех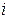 
и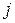 
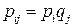, (3.10)
то есть вероятность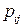 
факторизуется.
Если при каких-либо 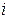и 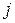равенство (3.10) не выполняется, то ДСВ и являются зависимыми.
(Случай счетного числа возможных значений у какой-либо из ДСВ или рассмотреть самостоятельно).
▲ Необходимость. Пусть дискретные случайные величины и являются независимыми. Тогда 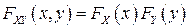для любых .
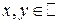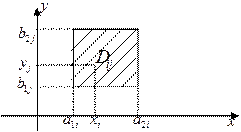
Обозначим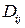 
прямоугольник
со сторонами, параллельными осям
координат, который содержит точку
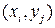и не содержит других значений
.
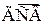
Тогда
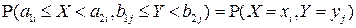(по построению ) =
= 
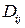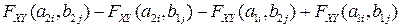(по свойству 4) =
= 
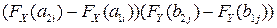(в силу независимости случайных величин) = 
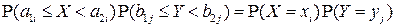(по построению ),
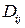то есть 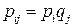, и так можно сделать для любого значения .
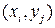Достаточность. Если выполняется равенство (3.10), то в соответствии с определениями ФР ,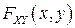 
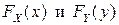имеем:
,
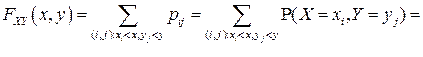
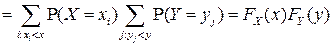то есть ДСВ и являются независимыми ■.
Лемма 2.
Пусть - 
, 
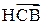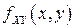- его ПВ, 
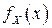и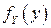 
- одномерные ПВ его координат, определяемые по формулам (3.8).
НСВ и являются независимыми тогда и только тогда, когда
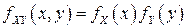(3.11)
для всех 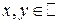, являющихся точками непрерывности функци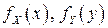й 
и 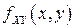, то есть двумерная ПВ 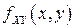факторизуется.
Если при каких-либо 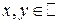равенство (3.11) не выполняется, то НСВ и являются зависимыми.
▲ Необходимость. Если НСВ и являются независимыми, то
.
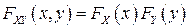Дифференцируя это равенство 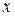по 
и по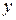 
, получаем:
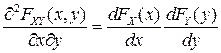
и, следовательно, в соответствии с определениями ПВ 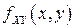, 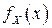и 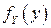, справедливо равенство:
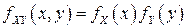
в точках непрерывности функци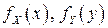й и .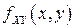
Достаточность. Проинтегрируем равенство (3.11) по первому аргументу в пределах от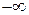 
до 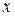и по второму аргументу в пределах от 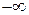до 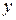. В результате получаем:
.
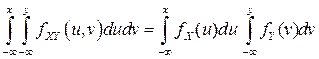и, следовательно, в соответствии с определениями ФР 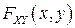, 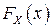и 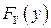для любых 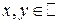справедливо равенство:
,
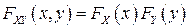то есть СВ и являются независимыми ■.
Леммы 1 и 2 показывают, что, если СВ и являются независимыми, то двумерный ЗР 
полностью определяется одномерными ЗР его координат (то есть понятие в этом случае вырождается).
Утверждения (3.10) и (3.11) лемм 1 и 2 сами могут служить определениями независимости СВ в дискретном и непрерывном случаях соответственно.
Пример.
а) Равномерное распределение в прямоугольнике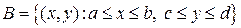 
со сторонами, параллельными осям координат.
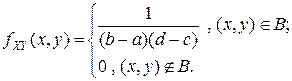
Ранее были найдены одномерные ПВ координат:
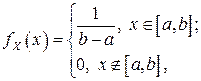
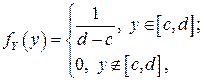
Поскольку в этом случае 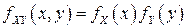, то СВ и являются независимыми.
б) Равномерное распределение в круге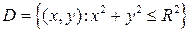 
.
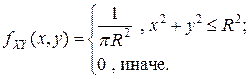
Ранее были найдены одномерные ПВ координат:
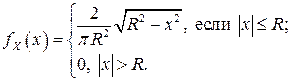
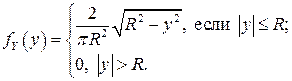
Поскольку в данном случае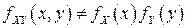 
, то СВ и являются зависимыми.
Понятие независимости СВ обобщается на любое конечное число СВ следующим образом.
Определение. СВ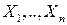 
называются независимыми в совокупности, если для любого 
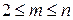, для любого набора индексов 
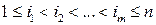и для любых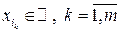 
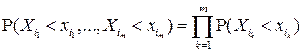
или в терминах ФР для любой точки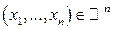 
,
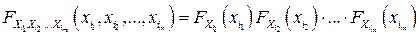где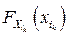 
– ФР СВ 
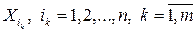, то есть многомерная ФР 
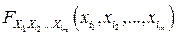факторизуется.
Для независимости в совокупности непрерывных случайных величин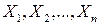 
, имеющих плотности вероятностей 
, 
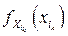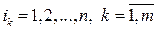необходимо и достаточно, чтобы
,
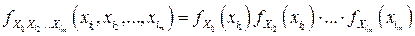во всех точках непрерывности функци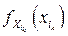й и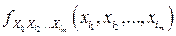 
, .
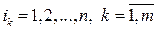Из независимости СВ в совокупности при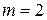 
следует их попарная независимость. Обратное неверно (примером тому по-прежнему служит пример Бернштейна С.Н., если в качестве СВ рассмотреть индикаторные СВ соответствующих событий). В дальнейшем при рассмотрении одновременно более двух СВ под их независимостью, по умолчанию, будет подразумеваться независимость в совокупности.
|
|