
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условные законы распределения и условные числовые характеристики
|
|
Известно, что, если случайные события А и В зависимы, то условная вероятность события А отличается от его безусловной вероятности. В этом случае
 .
.
Аналогичное положение имеет место и для СВ.
Пусть  и
и  - зависимые СВ,
- зависимые СВ, 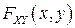 - их совместная ФР. Если известно, что СВ
- их совместная ФР. Если известно, что СВ  уже приняла некоторое значение y, то ЗР СВ
уже приняла некоторое значение y, то ЗР СВ  при этом условии не будет совпадать с ее безусловным ЗР. Он называется условным законом распределения (УЗР) СВ
при этом условии не будет совпадать с ее безусловным ЗР. Он называется условным законом распределения (УЗР) СВ  при условии, что
при условии, что  , и, заданный для всех возможных значений y СВ
, и, заданный для всех возможных значений y СВ  , полностью определяет зависимость между СВ
, полностью определяет зависимость между СВ  и
и  .
.
Исчерпывающей характеристикой УЗР СВ  при условии, что
при условии, что  , является условная ФР
, является условная ФР  (УФР) СВ
(УФР) СВ  при условии, что
при условии, что  , которую естественно было бы определить как
, которую естественно было бы определить как
 . (3.12)
. (3.12)
Следует отметить, что это определение не имеет смысла, если  , что имеет место всегда, когда
, что имеет место всегда, когда  - НСВ. Тем не менее, в дискретном случае определением (3.12) можно вполне пользоваться.
- НСВ. Тем не менее, в дискретном случае определением (3.12) можно вполне пользоваться.
Пусть  -
- 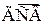 ,
,  - его возможные значения,
- его возможные значения,  - вероятности значений,
- вероятности значений,  ,
,  ,
,  (случай счетного числа значений
(случай счетного числа значений 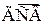 рассмотреть самостоятельно). Тогда все УЗР СВ
рассмотреть самостоятельно). Тогда все УЗР СВ  при условии, что
при условии, что 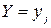 ,
,  , являются дискретными и согласно определению условной вероятности имеем:
, являются дискретными и согласно определению условной вероятности имеем:
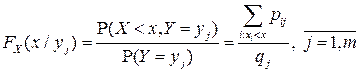 .
.
Дискретные УЗР удобнее задавать не УФР  , а совокупностью условных вероятностей
, а совокупностью условных вероятностей 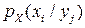 , заданных при каждом
, заданных при каждом  :
:

и записывать в виде таблицы:

| 
| 
| 
| 
|

| 
| 
| 
| 
|
Очевидно, что при этом выполняется условие нормировки:
 .
.
Аналогичны выражения для УФР  , условных вероятностей
, условных вероятностей  и дискретного УЗР СВ
и дискретного УЗР СВ  при условии, что
при условии, что 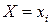 :
:
 ;
;
 ;
;

| 
| 
| 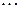
| 
|

| 
| 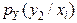
| 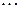
| 
|
Для вероятностей в последней таблице также выполняется условие нормировки:
 .
.
Рассмотрим теперь непрерывный случайный вектор  . Так как в этом случае
. Так как в этом случае  при любом
при любом  , то определение (3.12) условной функции распределения
, то определение (3.12) условной функции распределения  случайной величины
случайной величины  при условии, что
при условии, что  , неприменимо. Для непрерывных случайных величин
, неприменимо. Для непрерывных случайных величин  и
и  условную функцию распределения
условную функцию распределения  определяют следующим образом:
определяют следующим образом:
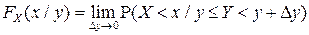 .
.
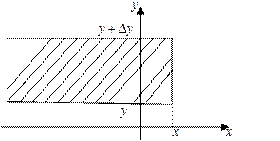 Вероятность, стоящая под знаком
Вероятность, стоящая под знаком
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
предела, представляет собой
вероятность попадания непрерывного
случайного вектора  в полосу.
в полосу.
В соответствии с определением условной вероятности и свойствами двумерной ФР имеем:



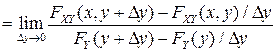 .
.
Если последний предел существует, то он равен
 .
.
Учитывая, что у 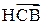
 существует ПВ
существует ПВ 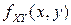 и
и  , а также, что у СВ
, а также, что у СВ  существует ПВ
существует ПВ  и
и  , для УФР
, для УФР  получаем выражение:
получаем выражение:
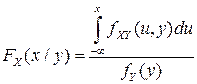 (3.13)
(3.13)
в точках непрерывности функций 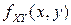 и
и  .
.
Условная ПВ 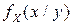 (УПВ) СВ
(УПВ) СВ  при условии, что
при условии, что  , по аналогии с одномерным случаем определяется как производная по х от УФР
, по аналогии с одномерным случаем определяется как производная по х от УФР  :
:
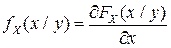
в точках, где УПВ 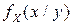 непрерывна.
непрерывна.
Из (3.13) следует, что
 (3.14)
(3.14)
(при этом полагается, что  , если
, если  ).
).
Аналогичные выражения имеют место для УФР  и УПВ
и УПВ  СВ
СВ  при условии, что
при условии, что 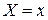 :
:
 ; (3.15)
; (3.15)
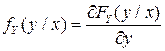
в точках, где УПВ  непрерывна;
непрерывна;
 (3.16)
(3.16)
(при этом полагается, что  , если
, если  ).
).
Как и любая ПВ, УПВ обладают свойствами:
При фиксированном y
 ;
;  (условие нормировки);
(условие нормировки);
При фиксированном х
 ;
;  (условие нормировки).
(условие нормировки).
Формулы (3.14) и (3.16) дают выражения для УПВ через безусловные, их также можно записать в виде:

Полученная формула есть правило умножения ПВ, которая является обобщением известного правила умножения вероятностей.
Для СВ в терминах ПВ имеют место также аналоги формулы полной вероятности и формулы Байеса:
 ;
;

(в последней формуле  - априорная ПВ, а
- априорная ПВ, а  - апостериорная ПВ).
- апостериорная ПВ).
Используя понятие УЗР, получаем еще одно эквивалентное определение независимости СВ.
Для независимости СВ  и
и  необходимо и достаточно, чтобы УЗР одной из СВ относительно другой совпадали с безусловными (аналог равенств
необходимо и достаточно, чтобы УЗР одной из СВ относительно другой совпадали с безусловными (аналог равенств  ):
):
 ,
, 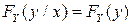 ;
;
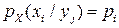 ,
,  ;
;
 ,
,  .
.
Кратко о многомерном случае. Здесь возникает дополнительная возможность рассмотрения УЗР одной группы координат  относительно другой. Но при этом определения полностью аналогичны.
относительно другой. Но при этом определения полностью аналогичны.
Так, например, УПВ «отрезка»  вектора
вектора 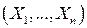 при условии, что СВ
при условии, что СВ  приняли определенные значения
приняли определенные значения  , задается формулой:
, задается формулой:
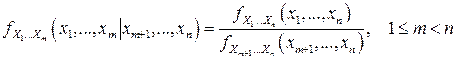 .
.
Условные числовые характеристики (математическое ожидание и дисперсия) определяются и находятся также, как и безусловные, только в формулах для их вычисления следует безусловные законы распределения заменить на условные.
Если  -
- 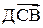 , то условным математическим ожиданием СВ
, то условным математическим ожиданием СВ  при условии, что
при условии, что 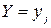 , называется величина
, называется величина

а условным математическим ожиданием СВ  при условии, что
при условии, что 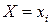 , - величина
, - величина

Если  -
- 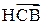 , то условные математические ожидания СВ
, то условные математические ожидания СВ  при условии, что
при условии, что  , и СВ
, и СВ  при условии, что
при условии, что 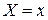 , определяются формулами:
, определяются формулами:
 ;
;
 .
.
Аналогичные формулы имеют место и для условных дисперсий.
Если  -
- 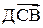 , то
, то
 ;
;
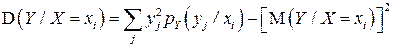 .
.
Если  -
- 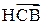 , то
, то
 ;
;
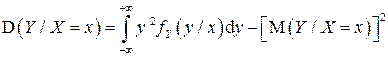 .
.
Отметим, что, если безусловные МО и дисперсия являются числами, то условные МО и дисперсия есть функции условия. Функцию  называют также функцией регрессии
называют также функцией регрессии  на
на  , а функцию
, а функцию  - функцией регрессии
- функцией регрессии  на
на  .
.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|
