
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Случайные векторы. Функция распределения случайного вектора и ее свойства.
|
|
Часто в вероятностных моделях случайных явлений приходится рассматривать сразу несколько СВ, причем изучение каждой СВ отдельно от других приводит к недопустимому упрощению модели. Математической моделью таких случайных явлений является понятие случайного вектора (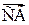 ).
).
Определение. Совокупность случайных величин 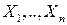 , значения которых совместно описывают результат некоторого случайного явления, называется
, значения которых совместно описывают результат некоторого случайного явления, называется 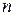 -мерным случайным вектором (многомерной СВ или системой СВ) и обозначается
-мерным случайным вектором (многомерной СВ или системой СВ) и обозначается 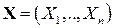 . При этом сами СВ
. При этом сами СВ 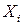 ,
, 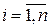 называют координатами (компонентами, составляющими)
называют координатами (компонентами, составляющими) 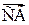
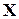 .
.
Исчерпывающей вероятностной характеристикой 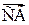 является его функция распределения (ФР). Рассмотрим вначале случай двумерного случайного вектора
является его функция распределения (ФР). Рассмотрим вначале случай двумерного случайного вектора 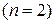 , как наиболее часто встречающийся в практических приложениях, а потом полученные результаты обобщим на случай многомерный.
, как наиболее часто встречающийся в практических приложениях, а потом полученные результаты обобщим на случай многомерный.
Двумерный 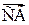 обычно обозначают
обычно обозначают 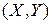 (без введения индексов).
(без введения индексов).
Определение. ФР 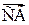
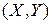 называется функция
называется функция  двух действительных переменных
двух действительных переменных 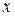 и
и 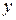 , определяемая при каждом
, определяемая при каждом 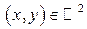 равенством:
равенством:
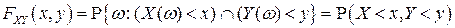 . (3.1)
. (3.1)
ФР 
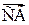
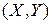 называют также двумерной ФР или совместной ФР СВ
называют также двумерной ФР или совместной ФР СВ  и
и  .
.
Геометрически ФР  представляет собой вероятность попадания случайной точки
представляет собой вероятность попадания случайной точки 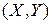 в квадрант с вершиной в точке
в квадрант с вершиной в точке 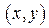 .
.

Из определения (3.1) вытекают следующие свойства ФР  .
.
Свойства двумерной ФР.
1. 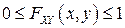 для любых
для любых 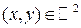 .
.
(свойство очевидно, так как ФР  - вероятность).
- вероятность).
2. 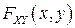 является неубывающей функцией по каждому из своих аргументов.
является неубывающей функцией по каждому из своих аргументов.
▲ Когда один из аргументов 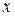 или
или 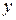 фиксирован, доказательство свойства 2 полностью аналогично одномерному случаю. ■.
фиксирован, доказательство свойства 2 полностью аналогично одномерному случаю. ■.
3. 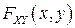 является непрерывной слева функцией по каждому из своих аргументов.
является непрерывной слева функцией по каждому из своих аргументов.
▲ Когда один из аргументов 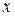 или
или 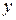 фиксирован, доказательство свойства 3 полностью аналогично одномерному случаю ■.
фиксирован, доказательство свойства 3 полностью аналогично одномерному случаю ■.
4. 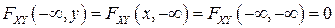 ;
; 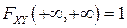 .
.
▲ В силу свойства 5 вероятности
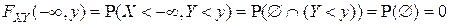 ;
;
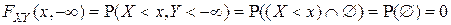 ;
;
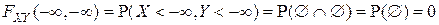 .
.
В силу аксиомы нормированности
 ■.
■.
5. 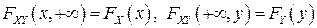 ,
,
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
где 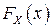 и
и 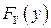 - функции распределения координат
- функции распределения координат  и
и  соответственно.
соответственно.
Свойство 5 означает, что по функции распределения двумерного случайного вектора  всегда можно найти одномерные (маргинальные) функции распределения его координат. Обратное без дополнительной информации неверно.
всегда можно найти одномерные (маргинальные) функции распределения его координат. Обратное без дополнительной информации неверно.
▲ В соответствии со свойствами вероятности имеем:
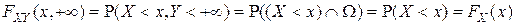 ;
;
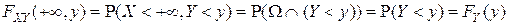 ■.
■.
6. Вероятность попадания случайного вектора  в прямоугольник
в прямоугольник 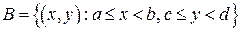 со сторонами, параллельными осям координат, определяется по формуле:
со сторонами, параллельными осям координат, определяется по формуле:

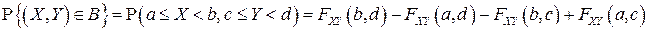 ▲ Обозначим
▲ Обозначим
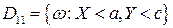 ;
;
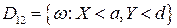 ;
;
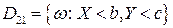 ;
;
 .
.
Очевидно, что  . При этом события
. При этом события 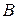 и
и 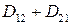 являются несовместными, а
являются несовместными, а 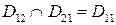 . Поэтому по теореме сложения вероятностей получаем:
. Поэтому по теореме сложения вероятностей получаем:
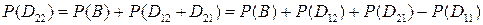 .
.
Остается теперь учесть, что 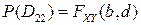 ,
, 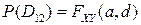 ,
,
 ,
, 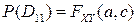 ■.
■.
Аналогичными являются определение и свойства многомерной ФР.
Определение. Функция 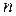 действительных переменных, определяемая для любого
действительных переменных, определяемая для любого 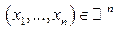 равенством
равенством
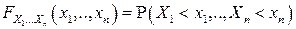 ,
,
называется функцией распределения случайного вектора 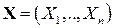 или многомерной (
или многомерной (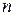 -мерной) ФР или совместной ФР СВ
-мерной) ФР или совместной ФР СВ 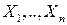 .
.
Свойства многомерной ФР.
1.  для любых
для любых 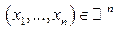 .
.
2. 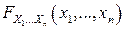 является неубывающей функцией по каждому из своих аргументов.
является неубывающей функцией по каждому из своих аргументов.
3. 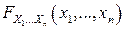 является непрерывной слева функцией по каждому из своих аргументов.
является непрерывной слева функцией по каждому из своих аргументов.
4. 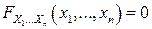 , если хотя бы один из аргументов
, если хотя бы один из аргументов 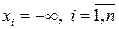 .
.
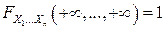 .
.
5. (Свойство согласованности). По ФР 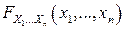
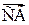
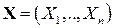 можно получить ФР любой совокупности
можно получить ФР любой совокупности 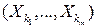 из
из 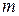
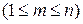 его координат. Для этого следует в ФР
его координат. Для этого следует в ФР 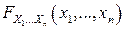 положить аргументы
положить аргументы 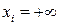 для
для 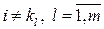 .
.
Многомерный аналог свойства 6 двумерной ФР приводить не будем из-за необходимости введения разностных операторов и его громоздкой записи.
В приложениях, как правило, имеют дело со 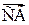 двух типов: дискретными и непрерывными. В каждом из этих случаев существуют более удобные, чем ФР, способы задания
двух типов: дискретными и непрерывными. В каждом из этих случаев существуют более удобные, чем ФР, способы задания 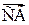 .
.
|
|
