
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон распределения дискретного случайного вектора
|
|
Определение. 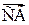
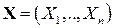 называется дискретным (
называется дискретным ( 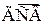 ), если множество его возможных значений конечно или счетно:
), если множество его возможных значений конечно или счетно:
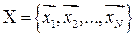 или
или 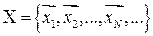 ,
,
где 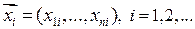 .
.
Из определения следует, что  является дискретным тогда и только тогда, когда все его координаты
является дискретным тогда и только тогда, когда все его координаты 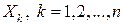 , являются ДСВ.
, являются ДСВ.
Рассмотрим более подробно случай двумерного 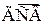
 , принимающего конечное число значений (случай счетного числа значений рассмотреть самостоятельно). Для полной вероятностной характеристики такого
, принимающего конечное число значений (случай счетного числа значений рассмотреть самостоятельно). Для полной вероятностной характеристики такого 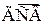
 достаточно указать все его возможные значения
достаточно указать все его возможные значения 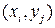 и вероятности
и вероятности 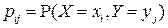 , с которыми эти значения принимаются,
, с которыми эти значения принимаются, 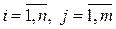 (предполагается, что СВ
(предполагается, что СВ  принимает
принимает 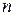 значений, а СВ
значений, а СВ  принимает
принимает 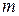 значений, так что у вектора
значений, так что у вектора  возможных значений
возможных значений 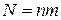 ).
).
Как и в одномерном случае, подобную информацию о 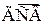
 записывают в виде таблицы, но с двумя входами:
записывают в виде таблицы, но с двумя входами:


| 
| 
| … | 
| (3.2) |

| 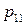
| 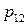
| … | 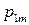
| |

| 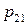
| 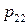
| … | 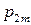
| |
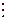
| 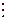
| 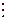
| 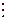
| 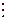
| |

| 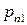
| 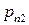
| … | 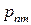
|
которую называют законом распределения (ЗР) 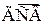
 (двумерным дискретным ЗР или совместным ЗР ДСВ
(двумерным дискретным ЗР или совместным ЗР ДСВ  и
и  ).
).
При этом, поскольку события 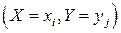 ,
, 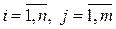 , образуют полную группу событий, то вероятности
, образуют полную группу событий, то вероятности 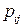 удовлетворяют условию нормировки:
удовлетворяют условию нормировки:

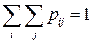 .
.
По двумерному закону распределения вероятность попадания дискретного случайного вектора  в любую область
в любую область 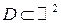 определяется по формуле:
определяется по формуле:
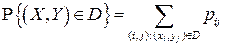 .
.
В частности, когда 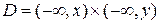 , получается следующее выражение для функции распределения
, получается следующее выражение для функции распределения 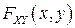
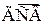
 :
:
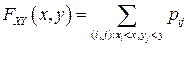 .
.
(ср. с одномерным случаем, когда 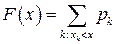 ).
).
График ФР 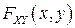
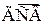
 является кусочно-постоянным со скачками в точках
является кусочно-постоянным со скачками в точках 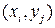 , являющихся его возможными значениями, величина скачков определяется вероятностями
, являющихся его возможными значениями, величина скачков определяется вероятностями 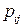
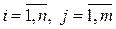 .
.
Одномерные ЗР каждой из СВ  и
и  в отдельности (маргинальные законы распределения)
в отдельности (маргинальные законы распределения) 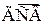
 являются дискретными и находятся по двумерному ЗР следующим образом:
являются дискретными и находятся по двумерному ЗР следующим образом:
Так как событие 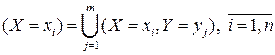 , то в силу аддитивности вероятности
, то в силу аддитивности вероятности
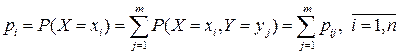 . (3.3)
. (3.3)
Таким образом, ЗР СВ  имеет вид:
имеет вид:

| 
| 
| 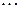
| 
|
| 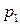
| 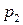
| 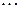
| 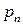
|
где в соответствии с (3.3) вероятность 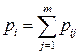 получается суммированием в
получается суммированием в 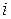 -ой строке таблицы (3.2) вероятностей
-ой строке таблицы (3.2) вероятностей 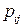 ,
, 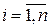 .
.
Аналогично, вероятности
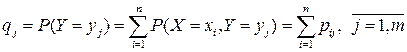 (3.4)
(3.4)
и поэтому ЗР СВ  имеет вид:
имеет вид:

| 
| 
| 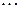
| 
|
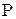
| 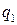
| 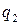
| 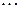
| 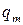
|
где в соответствии с (3.4) вероятность 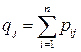 получается суммированием в
получается суммированием в 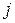 -ом столбце таблицы (3.2) вероятностей
-ом столбце таблицы (3.2) вероятностей 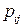 ,
,  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Многомерный случай 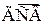
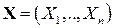 полностью аналогичен двумерному, только менее нагляден и имеет громоздкую индексацию. Так, ЗР
полностью аналогичен двумерному, только менее нагляден и имеет громоздкую индексацию. Так, ЗР 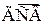
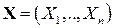 определяется набором вероятностей
определяется набором вероятностей 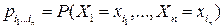 , где
, где 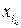 - значения координаты
- значения координаты 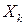 ,
, 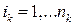 ,
, 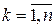 .
.
|
|
