Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача линейной регрессии и оценка по методу наименьших квадратов.

Задача линейной регрессии является частным случаем практической задачи, изложенной в предыдущем пункте, в котором априорно известно (или предполагается), что условное математическое ожидание является функцией линейно зависящей от параметра :

(9.1)

где – фиксированный, но неизвестный числовой вектор, и 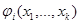– известные детерминированные функции (). В этом важном частном случае может быть получено уравнение для нахождения вектора параметров , при котором среднеквадратичное отклонение принимает наименьшее значение.

Из (9.1) следует, что:

, где ,

(9.2)

– -ая строка матрицы , и среднеквадратичное отклонение принимает вид:

.

Решение задачи нахождения вектора , при котором среднеквадратичное отклонение принимает наименьшее значение, дается методом наименьших квадратов, а сам вектор , называют оценкой по методу наименьших квадратов.

Необходимое условие экстремума как функции параметра заключается в равенстве частных производных нулю в точке :

, .

Вычислим частные производные:

, ,

, ,

,

(9.3)

Полученное уравнение называется нормальным уравнением метода наименьших квадратов. Нормальное уравнение играет роль необходимого условия: «если принимает наименьшее значение в точке , тогда удовлетворяет нормальному уравнению ». Отсюда следует, что среди всех решений нормального уравнения есть решения, доставляющие минимальное значение среднеквадратичному отклонению. Однако, отсюда еще не следует, что любое решение нормального уравнения будет доставлять минимальное значение среднеквадратичному отклонению. Тем не менее, оказывается, что это действительно так, необходимое условие в некоторых случаях является достаточным: «если удовлетворяет нормальному уравнению , тогда принимает наименьшее значение в точке », доказательству этого факта посвящено утверждение 9.2, основанное на утверждении 9.1.