Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 9.1.

Для матрицы порядка :

1) матрица 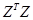неотрицательно определена, ;

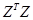2) если и ранг матрицы равен , тогда матрица положительно определена, .

Утверждение 9.2.

Пусть – вектор порядка и – матрица порядка , где , если – решение нормального уравнения:

,

тогда,

.

Если дополнительно ранг матрицы равен , тогда решение нормального уравнения единственно, дается равенством , и является единственным вектором, при котором принимает наименьшее значение.

Постановка задачи линейной регрессии с дополнительным предположением об остатках, теорема о свойствах оценки по методу наименьших квадратов, утверждение об оценке остаточной дисперсии. Понятия коэффициента детерминации и скорректированного коэффициента детерминации.

Пусть известно, что выполняется (9.1), тогда наблюдение имеет вид:

, …, ,

(9.4)

Будем дополнительно предполагать, что случайные величины , …, имеют следующие свойства:

1) 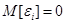, ; 2) , ; 3) , , .

(9.5)

Предположим, что на основании результатов предыдущего пункта получена оценка по методу наименьших квадратов . Оценка , зависящая от наблюдения , является векторной случайной величиной, поэтому возникает вопрос о свойствах оценки и о том каким образом связаны между собой оценка и неизвестный вектор параметров .