Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Следствие

При выполнении условий теоремы 4.12 статистика является состоятельной оценкой -квантиля , поскольку математическое ожидание 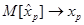и дисперсия при .

Пусть функция распределения зависит от неизвестного параметра , для построения оценки величины с помощью порядковых статистик достаточно выразить величину через квантили функции распределения :

.

Использование вместо квантилей , …, их оценок, полученных с помощью порядковых статистик, , …, , приводит к статистике:

,

которая используется в качестве оценки .

При некоторых условиях статистики являются состоятельными оценками квантилей , то есть имеет место сходимость по вероятности при 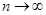, если функция 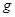непрерывна в точке , тогда по свойству сходимости по вероятности статистика сходится по вероятности к величине :

, при ,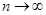

тогда по определению статистика является состоятельной оценкой .

Оценки, полученные методом порядковых статистик, как правило, имеют дисперсию больше, чем дисперсии оценок, полученные другими методами. Тем не менее, оценки, полученные методом порядковых статистик, могут обладать дополнительными положительными свойствами, например, устойчивостью к «засорению» выборки («засорение» выборки означает наличие в выборке ошибочных значений, полученных в результате неверного измерения и т.п.)

Понятие доверительного интервала, верхней и нижней доверительных границ. Понятие центральной статистики и общий метод построения доверительных интервалов с помощью центральной статистики. Метод построения центральной статистики.

Всякая точечная оценка сообщает лишь одно значение, которое принимается за приближенное значение оцениваемой величины, при этом полученное значение в большинстве случаев, конечно, не совпадает с истинным значением оцениваемой величины, поэтому в ряде случаев требуется указать интервал, в котором с большой вероятностью находится оцениваемая величина.

Пусть – наблюдение, – неизвестный скалярный параметр и 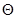– множество допустимых значений параметра .