Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение 5.4.

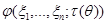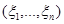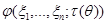Пусть – наблюдение и случайная величина зависит как от наблюдения так и от неизвестной величины . Случайная величина называется центральной статистикой для величины , если:

1) функция распределения 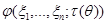известна (то есть никаким образом не зависит от неизвестного параметра ),

2) при всех реализациях наблюдения 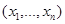одновременно функция 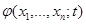непрерывна и строго монотонна по 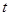(например, при всех 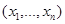функция 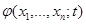непрерывна и возрастает по ).

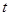Предположим, что некоторым образом построена центральная статистика для – 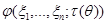, поскольку функция распределения 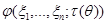известна (условие 1), то всегда можно найти числа 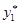и 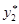такие, что:

.

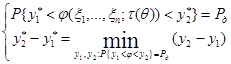Поскольку функция 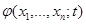непрерывна по 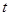при всех реализациях наблюдения 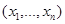, то при каждом 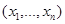существуют решения 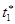и системы уравнений (рисунок 5.1):

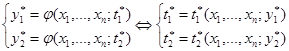
Рисунок 5.1.

Если функция 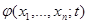возрастает по 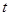при всех реализациях наблюдения, тогда события 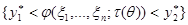и 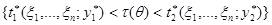эквивалентны и вероятности событий равны, то есть:

.

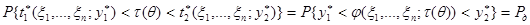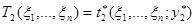Пусть статистики и , тогда интервал 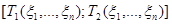является доверительным интервалом для с уровнем доверия 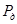, поскольку для всех допустимых значений параметра :

,

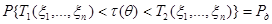следовательно,

.

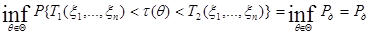Если функция 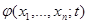убывает по 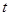при всех реализациях наблюдения, тогда эквивалентны события 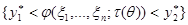и 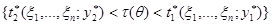и равны вероятности:

.

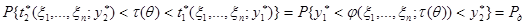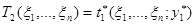Пусть статистики и , тогда интервал 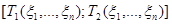является доверительным интервалом для с уровнем доверия , поскольку для всех допустимых значений параметра :

,

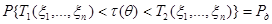тогда,

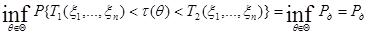
Аналогичным образом, с помощью центральной статистики 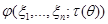могут быть построены доверительные границы.