Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 4.10.

Пусть – функция распределения, - квантиль (квантиль уровня ) функции распределения есть число такое, что:

.

(если существует несколько значений , удовлетворяющих условию , то в качестве -квантили принимают наименьшее из этих значений).

Если распределение, соответствующее имеет название, то обычно говорят, например, «квантиль уровня нормального распределения с параметрами 0 и 1» или «квантиль уровня распределения хи-квадрат с 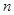степенями свободы».

Предположим, что функция распределения зависит от неизвестного параметра , тогда -квантиль является функцией параметра и является неизвестной величиной. Для построения оценки -квантили функцию распределения заменяют эмпирической функцией распределения .

Теорема 4.12. (Крамер)

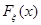Пусть – выборка из распределения , – -квантиль распределения 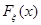и в некоторой окрестности точки плотность вероятности непрерывно дифференцируема и положительна, 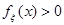, тогда статистика имеет асимптотически нормальное распределение:

, при .