
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 4.6.
|
|
Статистика 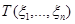 называется асимптотически нормальной с параметрами
называется асимптотически нормальной с параметрами  и
и 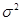 :
:
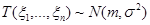 при
при 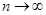 ,
,
если при каждом 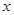 :
:
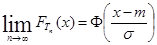 ,
,
где  – функция распределения
– функция распределения 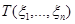 ,
,  – функция Лапласа (функция распределения нормальной случайной величины с математическим ожиданием 0 и дисперсией 1).
– функция Лапласа (функция распределения нормальной случайной величины с математическим ожиданием 0 и дисперсией 1).
Теорема 4.7. (асимптотические свойства МП-оценок)
Пусть 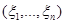 – выборка из распределения с плотностью вероятностью
– выборка из распределения с плотностью вероятностью 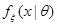 , зависящей от скалярного параметра
, зависящей от скалярного параметра  ,
, 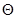 – множество допустимых значений параметра,
– множество допустимых значений параметра,  – истинное значение параметра,
– истинное значение параметра,  – МП-оценка параметра
– МП-оценка параметра  .
.
Если,
1) при каждом 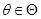 и почти всех
и почти всех 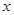 существуют производные
существуют производные  ,
, 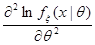 и
и 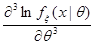 ;
;
2) при каждом 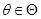 и почти всех
и почти всех 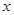 :
:  и
и 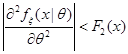 , причем существуют интегралы
, причем существуют интегралы 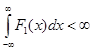 и
и 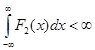 ;
;
3) при каждом 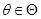 и почти всех
и почти всех 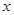 :
: 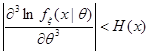 и существует единая постоянная
и существует единая постоянная 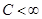 такая, что для всех
такая, что для всех 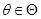 :
: 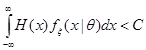 .
.
4) при каждом 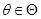 конечен и положителен интеграл:
конечен и положителен интеграл:
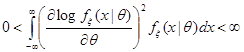
Тогда,
1) МП-оценка 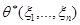 состоятельна, то есть
состоятельна, то есть 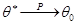 при
при 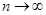 ;
;
2) МП-оценка 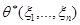 является асимптотически нормальной;
является асимптотически нормальной;
3) МП-оценка 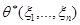 асимптотически эффективная;
асимптотически эффективная;
Метод порядковых статистик: построение оценок и оценка квантилей. Понятие порядковой статистики, функция распределения и функция плотности вероятности (без доказательства) порядковых статистик. Теорема Крамера об асимптотической нормальности порядковых статистик и свойства оценок по методу порядковых статистик.
Пусть  – выборка из распределения
– выборка из распределения 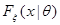 , тогда функция распределения
, тогда функция распределения 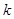 -ой порядковой статистики
-ой порядковой статистики 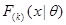 :
:
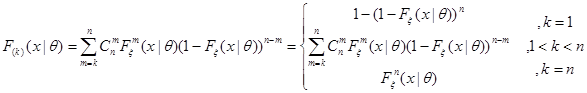
Доказательство:
Выберем произвольным образом и зафиксируем значение 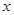 , определим на основе выборки
, определим на основе выборки 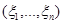 вектор бинарных случайных величин
вектор бинарных случайных величин 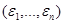 :
:
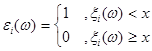 .
.
Случайные величины 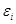 независимы в совокупности (поскольку случайные величины
независимы в совокупности (поскольку случайные величины  независимы в совокупности) и имеют одинаковое распределение
независимы в совокупности) и имеют одинаковое распределение  (поскольку случайные величины
(поскольку случайные величины  имеют одинаковую функцию распределения):
имеют одинаковую функцию распределения):
 ,
,
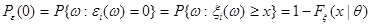 .
.
Пусть 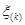 –
– 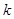 -ая порядковая статистика, по определению функция распределения
-ая порядковая статистика, по определению функция распределения 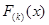 :
:
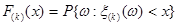 .
.
Порядковая статистика 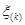 меньше величины
меньше величины 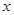 тогда и только тогда, когда среди величин выборки
тогда и только тогда, когда среди величин выборки 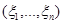
 (
(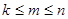 ) величин меньше
) величин меньше 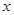 и
и 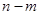 величин не меньше
величин не меньше 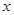 , то есть тогда и только тогда, когда в векторе бинарных случайных величин
, то есть тогда и только тогда, когда в векторе бинарных случайных величин 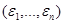
 величин равны 1 и
величин равны 1 и 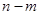 величин равны 0, что эквивалентно тому, что случайная величина
величин равны 0, что эквивалентно тому, что случайная величина  больше или равна
больше или равна 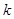 . Поскольку все
. Поскольку все 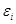 независимы и одинаково распределены, то случайная величина
независимы и одинаково распределены, то случайная величина 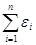 имеет распределение Бернулли с параметрами
имеет распределение Бернулли с параметрами 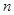 и
и 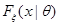 , тогда:
, тогда:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
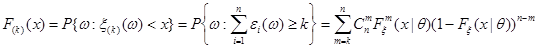
| (4.13) |
Заметим, что полученное равенство справедливо для любого  , поскольку величина
, поскольку величина  была выбрана произвольным образом.
была выбрана произвольным образом.
При  из (4.13) получим:
из (4.13) получим:
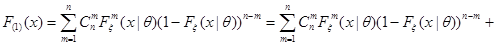
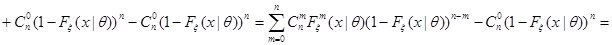
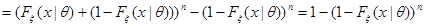 .
.
При  из (4.13) получим:
из (4.13) получим:
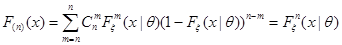 .
.
Утверждение доказано.
|
|
