Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 3.14.

Пусть – оптимальная оценка в классе несмещенных оценок (то есть – эффективная оценка ) и – статистика достаточная для параметра , тогда статистика является функцией :

,

где 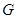некоторая функция.

Доказательство:

Определим статистику следующим образом:

,

тогда по теореме 3.13 оценка является несмещенной:

,

и кроме того,

.

Оценка является оптимальной в классе несмещенных оценок , и следовательно среди всех несмещенных оценок имеет наименьшую дисперсию, поэтому для всякой несмещенной оценки, в том числе и для :

Из двух неравенств следует, что

.

Таким образом, статистика также является оптимальной оценкой в классе несмещенных оценок , но несмещенная оптимальная оценка единственна (утверждение 1.12), отсюда статистики и совпадают:

.

Статистика является условным математическим ожиданием, и следовательно является функцией , поэтому:

.

Утверждение доказано.