
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Распределение хи-квадрат и построение доверительных интервалов для дисперсии и среднеквадратичного отклонения нормального распределения с известным математическим ожиданием.
|
|
Пусть 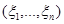 – выборка из нормального распределения с известным математическим ожиданием
– выборка из нормального распределения с известным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией 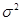 , построим доверительный интервал для дисперсии
, построим доверительный интервал для дисперсии 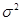 с уровнем доверия
с уровнем доверия  .
.
Рассмотрим статистику  :
:
 .
.
Поскольку случайные величины 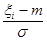 имеют нормальное распределение
имеют нормальное распределение  и независимы, то статистика
и независимы, то статистика 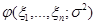 имеет распределение
имеет распределение 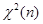 («хи-квадрат с
(«хи-квадрат с  степенями свободы») и кроме того одновременно при всех реализациях выборки
степенями свободы») и кроме того одновременно при всех реализациях выборки  функция
функция 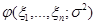 как функция параметра
как функция параметра 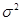 :
:
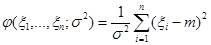
является непрерывной и убывающей. Таким образом, статистика 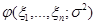 является центральной статистикой для
является центральной статистикой для 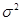 .
.
Для построения доверительного интервала выберем числа  и
и  так, чтобы выполнялось равенство:
так, чтобы выполнялось равенство:
 .
.
Для выполнения равенства достаточно, например, в качестве  взять квантиль уровня
взять квантиль уровня  распределения
распределения 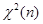 , а качестве
, а качестве  – квантиль уровня
– квантиль уровня  распределения
распределения 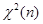 , действительно:
, действительно:
 ,
,
где  – случайная величина, имеющая распределение
– случайная величина, имеющая распределение 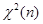 , и
, и  – функция распределения
– функция распределения  .
.
При таких значениях  и
и  получается так называемый «центральный интервал» (название обусловлено тем, что слева от
получается так называемый «центральный интервал» (название обусловлено тем, что слева от  «сосредоточена» вероятность
«сосредоточена» вероятность  и справа от
и справа от  «сосредоточена» вероятность
«сосредоточена» вероятность 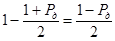 ). Построение «наикратчайшего» доверительного интервала, то есть нахождение чисел
). Построение «наикратчайшего» доверительного интервала, то есть нахождение чисел 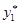 и
и 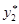 с наименьшей разностью
с наименьшей разностью  среди всех чисел удовлетворяющих
среди всех чисел удовлетворяющих  , в данном случае является технически сложным ([1] стр. 86), поэтому на практике ограничиваются более простым «центральным интервалом».
, в данном случае является технически сложным ([1] стр. 86), поэтому на практике ограничиваются более простым «центральным интервалом».
Преобразование неравенств приводит к следующему доверительному интевалу:
 ,
,
 ,
,
 .
.
Поскольку последнее равенство справедливо при всяком значении 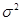 , то интервал:
, то интервал:
 ,
,
где  и
и  – квантили уровней
– квантили уровней  и
и  распределения
распределения 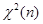 соответственно, является доверительным интервалом для
соответственно, является доверительным интервалом для 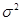 с уровнем доверия
с уровнем доверия 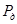 .
.
Нетрудно также получить и доверительный интервал для с.к.о. 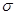 , действительно, поскольку:
, действительно, поскольку:
 ,
,
то
 ,
,
тогда при тех же значениях  и
и  интервал:
интервал:
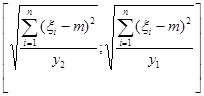
является доверительным интервалом для 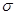 с уровнем доверия
с уровнем доверия 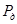 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Теорема Фишера о выборочном среднем и исправленной выборочной дисперсии. Построение доверительных интервалов для дисперсии и среднеквадратичного отклонения нормального распределения с неизвестным математическим ожиданием.
Теорема 5.5. (Фишер)
Пусть  – выборка из нормального распределения
– выборка из нормального распределения  , статистики
, статистики  и
и  , тогда:
, тогда:
1) Статистика 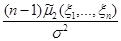 имеет распределение
имеет распределение  ;
;
2) Статистики 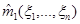 и
и  – независимые случайные величины.
– независимые случайные величины.
Доказательство:
1) Преобразуем статистику 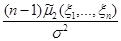 следующим образом:
следующим образом:
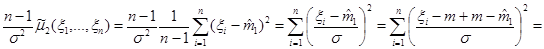


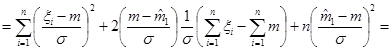
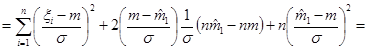
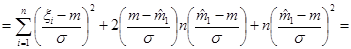
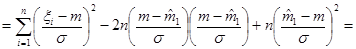

 .
.
Определим вектор-столбец случайных величин 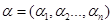 :
:
 ,
,
тогда,
 .
.
Поскольку случайные величины  имеют нормальное распределение, то случайные величины
имеют нормальное распределение, то случайные величины  также имеют нормальное распределение (как линейное преобразование нормальной случайной величины). Легко видеть, что математическое ожидание
также имеют нормальное распределение (как линейное преобразование нормальной случайной величины). Легко видеть, что математическое ожидание  есть нулевой вектор:
есть нулевой вектор:
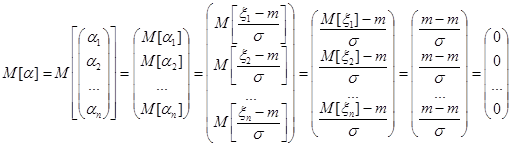 ,
,
и дисперсионная матрица  является единичной матрицей
является единичной матрицей  , поскольку:
, поскольку:

 ,
,
где  при
при  поскольку
поскольку  и
и 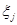 независимы (
независимы ( - выборка по условию теоремы).
- выборка по условию теоремы).
Пусть  – ортогональная матрица (т.е.
– ортогональная матрица (т.е.  , где
, где  – транспонированная матрица
– транспонированная матрица  ), в которой все элементы первой строки равны
), в которой все элементы первой строки равны  :
:

| (5.1) |
Определим вектор-столбец случайных величин  :
:
 ,
,
 .
.
Каждая случайная величина  имеет нормальное распределение, поскольку все
имеет нормальное распределение, поскольку все  имеют нормальное распределение. Математическое ожидание
имеют нормальное распределение. Математическое ожидание  есть нулевой вектор:
есть нулевой вектор:
 ,
,
и дисперсионная матрица  есть единичная матрица
есть единичная матрица  , поскольку:
, поскольку:
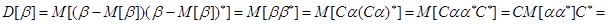
 ,
,
поскольку  – ортогональная матрица (
– ортогональная матрица ( ). Таким образом, случайные величины
). Таким образом, случайные величины  некоррелированные и поскольку все
некоррелированные и поскольку все  имеют нормальное распределение, то следовательно случайные величины
имеют нормальное распределение, то следовательно случайные величины  независимы.
независимы.
Покажем, что  , действительно:
, действительно:
 .
.
Из определения матрицы  (5.1):
(5.1):
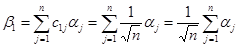
| (5.2) |
Таким образом,

| (5.3) |
где все величины  имеют нормальное распределение
имеют нормальное распределение  и независимы, поэтому статистика
и независимы, поэтому статистика  имеет распределение
имеет распределение  .
.
2) Из (5.2) следует:
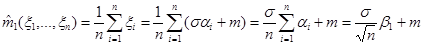
Из (5.3) следует:
 .
.
Поскольку случайные величины  независимы, то следовательно независимы
независимы, то следовательно независимы 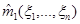 и
и  .
.
Теорема доказана.
Теорема 5.5 позволяет построить доверительный интервал для дисперсии нормального распределение в случае, когда математическое ожидание неизвестно. Пусть  – выборка из нормального распределения
– выборка из нормального распределения 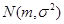 , из теоремы 5.5 следует, что статистика
, из теоремы 5.5 следует, что статистика  :
:
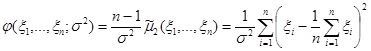
имеет распределение 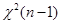 , не зависящее от неизвестных параметров
, не зависящее от неизвестных параметров  и
и 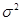 , и одновременно при всех реализациях выборки
, и одновременно при всех реализациях выборки  функция
функция  как функция
как функция 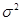 является непрерывной и убывающей. Следовательно, статистика
является непрерывной и убывающей. Следовательно, статистика 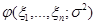 является центральной статистикой для
является центральной статистикой для 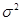 . Пусть
. Пусть  и
и  – квантили уровней
– квантили уровней  и
и  распределения
распределения 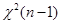 , тогда:
, тогда:
 ,
,
 ,
,
 .
.
Таким образом, интервал
 ,
,
где  и
и  являются квантилями уровней
являются квантилями уровней  и
и  распределения
распределения  , является доверительным интервалом для дисперсии
, является доверительным интервалом для дисперсии 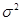 с уровнем доверия
с уровнем доверия 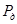 . Заметим, что при тех же значениях
. Заметим, что при тех же значениях  и
и  интервал
интервал
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
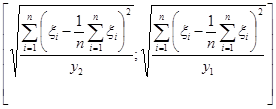
является доверительным интервалом для с.к.о. 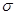 с уровнем доверия
с уровнем доверия 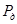 .
.
Формулировка теоремы Фишера о выборочном среднем и исправленной выборочной дисперсии. Построение доверительного интервала для математического ожидания нормального распределения с неизвестной дисперсией.
Теорема 5.5. (Фишер)
Пусть  – выборка из нормального распределения
– выборка из нормального распределения  , статистики
, статистики  и
и  , тогда:
, тогда:
1) Статистика 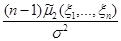 имеет распределение
имеет распределение  ;
;
2) Статистики 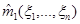 и
и  – независимые случайные величины.
– независимые случайные величины.
Пусть  – выборка из нормального распределения с неизвестным математическим ожиданием
– выборка из нормального распределения с неизвестным математическим ожиданием  и неизвестной дисперсией
и неизвестной дисперсией 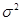 , построим доверительный интервал для
, построим доверительный интервал для  с уровнем доверия
с уровнем доверия 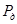 .
.
Рассмотрим статистику  :
:
 , ,
| (5.4) |
 ,
,  .
.
Заметим, что:
1) 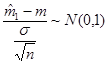 , поскольку все величины
, поскольку все величины  имеют нормальное распределение;
имеют нормальное распределение;
2)  и
и  независимы, поскольку в силу теоремы 5.5 статистики
независимы, поскольку в силу теоремы 5.5 статистики  и
и  независимы;
независимы;
3)  имеет распределение
имеет распределение  в силу теоремы 5.5.
в силу теоремы 5.5.
Из 1)-3) следует, что статистика  имеет распределение Стьюдента с
имеет распределение Стьюдента с  степенью свободы
степенью свободы  . Кроме того, при всех реализациях выборки
. Кроме того, при всех реализациях выборки  функция
функция  как функция
как функция  является непрерывной и убывающей, следовательно, случайная величина
является непрерывной и убывающей, следовательно, случайная величина  является центральной статистикой для
является центральной статистикой для  .
.
Пусть  и
и  – квантили уровней
– квантили уровней  и
и  распределения
распределения  , тогда:
, тогда:
 ,
,
 ,
,
 .
.
Поскольку распределение Стьюдента  является симметричным относительно нуля, то для функции распределения
является симметричным относительно нуля, то для функции распределения 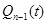 справедливо равенство:
справедливо равенство:
 .
.
Отсюда следует, что  , действительно:
, действительно:
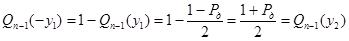 .
.
Таким образом,
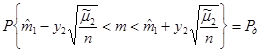
и следовательно интервал,
 ,
,
в котором 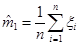 ,
,  и
и  – квантиль уровня
– квантиль уровня  распределения Стьюдента с
распределения Стьюдента с  степенью свободы, является доверительным интервалом для
степенью свободы, является доверительным интервалом для  с уровнем доверия
с уровнем доверия 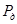 .
.
Построение доверительных интервалов с использованием асимптотической нормальности. Построение доверительного интервала для вероятности события (способ А до неравенства с квадратным уравнением, способы Б и В полностью). 3670
Пусть  – наблюдение и случайная величина
– наблюдение и случайная величина  имеет асимптотически (при
имеет асимптотически (при  ) нормальное распределение
) нормальное распределение  :
:
 , при
, при  ;
;
В силу асимптотической нормальности:
 , при
, при  ,
,
тогда при больших  справедливо приближенное равенство для вероятностей:
справедливо приближенное равенство для вероятностей:
 .
.
Пусть  является квантилью распределения
является квантилью распределения  уровня
уровня  , где
, где 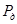 – уровень доверия:
– уровень доверия:
 ,
,
тогда,
 .
.
Разрешая неравенство относительно  , получим «приближенный» доверительный интервал:
, получим «приближенный» доверительный интервал:
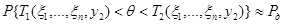 .
.
Воспользуемся вышеизложенным методом для построения «приближенного» доверительного интервала неизвестной вероятности события в схеме  независимых испытаний. Пусть
независимых испытаний. Пусть  – выборка, в которой каждая случайная величина
– выборка, в которой каждая случайная величина  является бинарной и принимает значение 1 с некоторой неизвестной вероятностью
является бинарной и принимает значение 1 с некоторой неизвестной вероятностью  и значение 0 с вероятностью
и значение 0 с вероятностью  :
:
 .
.
Требуется построить приближенный доверительный интервал для вероятности  . Рассмотрим случайную величину
. Рассмотрим случайную величину  :
:
 .
.
К случайным величинам  применима центральная предельная теорема, в соответствии с которой сумма
применима центральная предельная теорема, в соответствии с которой сумма 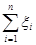 имеет асимптотически (при
имеет асимптотически (при  ) нормальное распределение с параметрами
) нормальное распределение с параметрами  , где:
, где:
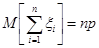 ,
,
 ,
,
тогда случайная величина:

имеет асимптотически (при  ) нормальное распределение
) нормальное распределение  :
:
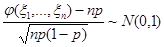 , при
, при  .
.
Пусть  – квантиль распределения
– квантиль распределения  уровня
уровня  , тогда при больших
, тогда при больших  :
:
 ,
,
 ,
,
 ,
,
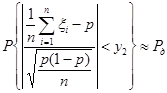 ,
,
 ,
,
где  . Разрешая неравенство относительно неизвестной вероятности
. Разрешая неравенство относительно неизвестной вероятности  , получим:
, получим:


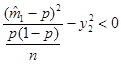
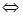
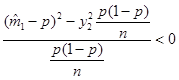
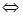

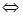

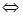

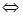

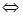
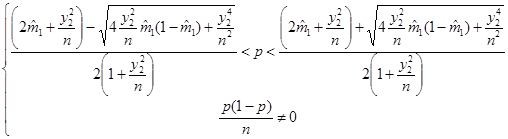
Пренебрегая слагаемыми с множителем  и с множителем
и с множителем  под корнем, получим приближенное неравенство:
под корнем, получим приближенное неравенство:
 ,
,
 ,
,
 .
.
Таким образом,
 ,
,
и «приближенный» доверительный интервал для вероятности  имеет вид:
имеет вид:
 ,
,
где 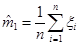 и
и  – квантиль распределения
– квантиль распределения  уровня
уровня  .
.
|
|
