Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Построение наикратчайшего доверительного интервала для математического ожидания нормального распределения с известной дисперсией.

Пусть – выборка из нормального распределения с неизвестным математическим ожиданием и известной дисперсией 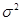, построим доверительный интервал для математического ожидания с уровнем доверия .

Поскольку все величины выборки имеют нормальное распределение, то статистика 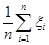также имеет нормальное распределение с параметрами:

,

.

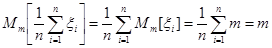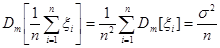Тогда статистика :

,

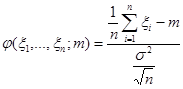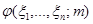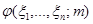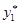имеет нормальное распределение не зависящее от неизвестного параметра и одновременно при всех реализациях функция как функция является непрерывной и убывающей. Согласно определению – центральная статистика для . Выберем числа и 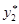так, чтобы выполнялись равенства:

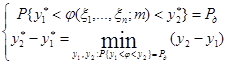
или

,

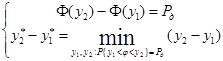где 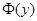- функция распределения нормальной случайной величины . Для нахождения минимума функции 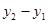при условии 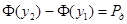воспользуемся методом Лагранжа, с функцией Лагранжа:

,

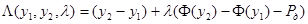которая приводит к системе:

.

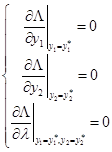
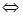
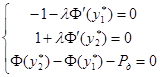
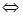
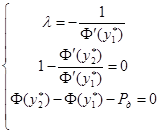
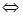
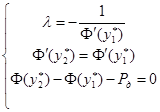
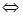
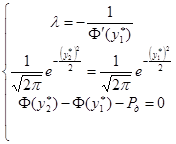
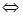
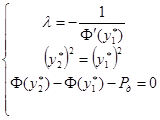У второго уравнения системы 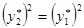или 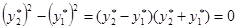, очевидно, имеется только два решения 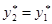и 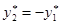, первое решение не удовлетворяет третьему уравнению системы 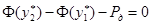, тогда:

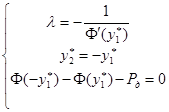
Используя свойство функции нормального распределения 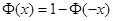получим:

.

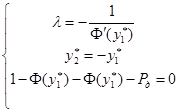
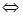
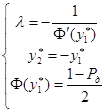Таким образом, 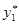есть квантиль уровня 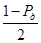распределения и 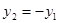. Значению 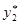можно придать иную интерпретацию:

,

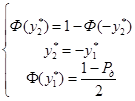
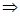
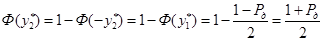то есть 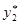является квантилью уровня 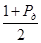распределения . Таким образом, получим равенство для вероятностей:

.

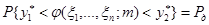Преобразовывая неравенства, получим:

,

.

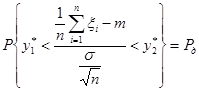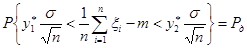
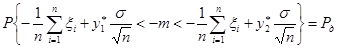
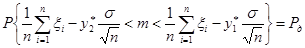Преобразование неравенств фактически является нахождением решения системы:

.

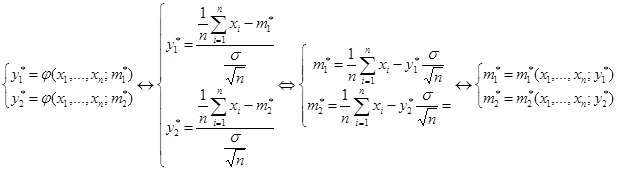Таким образом, при всяком значении параметра :

,

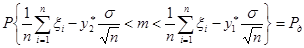тогда интервал ():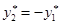

,

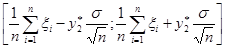где 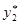– является квантилью уровня 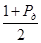распределения , является доверительным интервалом для с уровнем доверия .