Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 4.1.

Оценки , …, в системе (4.1) называются оценками, полученными по методу моментов (кратко, моментными оценками).

Моментные оценки , …, в общем случае не обладают свойством несмещенности (тем не менее, в некоторых частных случаях моментные оценки оказываются несмещенными).

Если функция 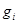(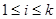) непрерывна в точке , то моментная оценка является состоятельной. Действительно, оценки начальных и центральных моментов являются состоятельными, откуда в силу свойства сходимости по вероятности, непрерывная функция от оценок , имеющих пределом по вероятности , сходится по вероятности к величине , таким образом:

,

что означает состоятельность оценоки .

Если в качестве используются первые начальных моментов функции распределения , функции , …, непрерывно дифференцируемы и функция распределения имеет моментов, то моментные оценки 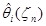имеют асимптотически нормальное распределение:

,

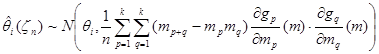где – вектор начальных моментов.

Моментные оценки в большом количестве случаев не являются эффективными и оптимальными, тем не менее, метод построения оценок оказывается простым и сами выражения для моментных оценок (4.1), как правило, оказываются простыми для вычисления.

Метод максимального правдоподобия построения точечных оценок. Утверждения о связи между МП-оценками, эффективными оценками и достаточными статистиками. Асимптотические свойства МП-оценок: несмещенность, нормальность и эффективность.

Пусть 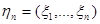– наблюдение (не обязательно выборка) и – плотность вероятности (или вероятность в дискретном случае) вектора , которая зависит от неизвестного вектора параметров . В результате проведения эксперимента будет получен числовой вектор , подставляя который в функцию , получим функцию, зависящую только от вектора (функцию правдоподобия – определение 3.1). При одних значениях параметра значение функции правдоподобия оказывается мало, при других значениях – велико. Поскольку значение функция правдоподобия отражает вероятность получения заданного вектора , то волне естественно выбрать параметр 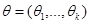так, чтобы вероятность получения наблюдаемого значения оказалось бы наибольшей.