Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Построение доверительного интервала для коэффициента корреляции двумерного нормального распределения с неизвестными математическими ожиданиями и дисперсиями.

Пусть выборка из двумерного нормального распределения с неизвестными математическими ожиданиями и , и неизвестными дисперсиями и . Требуется построить доверительный интервал для коэффициента корреляции с уровнем доверия .

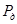Если случайная величина имеет распределение , то коэффициент корреляции :

.

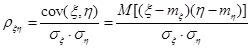Моментная оценка коэффициента корреляции имеет вид:

,

, .

Можно показать, что статистика имеет асимптотически нормальное распределение , однако, использовать непосредственно статистику для построения доверительного интервала весьма затруднительно, поскольку зависимость дисперсии от в конечном счете приводит к необходимости решать громоздкое квадратное уравнение. Во избежание указанной проблемы прибегают к преобразованию Фишера:

.

Можно показать, что статистика имеет асимптотически нормальное распределение , где и 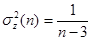не зависит от . Легко видеть, что случайная величина :

будет иметь асимптотически нормальное распределение и поэтому может быть использована для построения «приближенного» доверительного интервала. Для этого достаточно вычислить – квантиль распределения с уровнем доверия , тогда:

.

Разрешая неравенства относительно , получим статистики и (значения статистик вычисляют численными методами):

,

откуда непосредственно будет получен доверительный интервал .

Основные определения в задачах проверки статистических гипотез: статистическая гипотеза (простая и сложная), основная и альтернативная гипотезы (альтернативные распределения), статистический критерий и статистика критерия, критическая область и общий принцип проверки гипотез.

См25 хз что хотят куда всунуть

Основные определения в задачах проверки статистических гипотез: статистика критерия и критическая область, вероятности ошибок первого и второго родов, функция мощности критерия (функции мощности как характеристика критерия и вид функции мощности «хорошего» критерия), свойства несмещенности и состоятельности критерия.

Билеты из себя представляют сбор определений которые объяснены на тупом примере. Что из этого оставлять что убирать – сам черт ногу сломит. При формировании шпор по моему мнению нужно оставить только определения и чё нить попробовать наболтать

Одной из основных задач статистики является задача проверки статистических гипотез различного вида.