Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема об улучшении несмещенных оценок с помощью достаточных статистик (теорема Блекуэлла). Утверждение об оптимальной несмещенной оценке и достаточной статистике.

Теорема 3.13 (Блекуэлл)

Пусть – несмещенная оценка , – статистика, достаточная для параметра и случайная величина является условным математическим ожиданием величины при условии :

,

тогда

1) случайная величина является статистикой;

2) ;

3) .

Доказательство:

1) Заметим, что условная случайная величина:

(3.6)

где условное распределение случайного вектора при условии . Поскольку является статистикой достаточной для параметра , то по определению, условная плотность от параметра не зависит. Таким образом, справа в (3.6) под интегралом расположены функции, которые от параметра не зависят, и следовательно интеграл является функцией только , поэтому случайная величина , является статистикой, поскольку зависит только от наблюдения :

.

2) Вычислим математическое ожидание , воспользовавшись свойством условного математического ожидания:

,

поскольку является несмещенной оценкой .

3) Представим дисперсию с помощью условного математического ожидания и условной дисперсии:

.

Во втором слагаемом справа , поэтому:

,

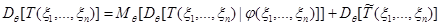поскольку условная дисперсия неотрицательна случайная величина, , то и математическое ожидание от неотрицательной величины условной дисперсии неотрицательно, :

.

Теорема доказана.