Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение 3.11.

Статистика называется достаточной для параметра , если условная плотность вероятности (или условная вероятность в дискретном случае) случайного вектора при условии не зависит от параметра .

Теорема 3.12. (критерий факторизации)

Пусть 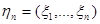– наблюдение и – функция правдоподобия вектора . Статистика является достаточной для параметра тогда и только тогда, когда функция правдоподобия имеет вид:

,

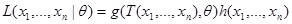где 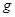и некоторые функции.

Доказательство:

Рассмотрим доказательство для только для случая, когда все случайные величины () дискретны.

1) Пусть статистика является достаточной для параметра , покажем, что:

.

Функция правдоподобия равна вероятности события :

.

Рассмотрим событие . Легко видеть, что если при некотором выполняются равенства ,..., , то при этом же выполняется равенство , поэтому, очевидно:

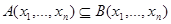
откуда следует, что совместное наступление событий и есть событие :

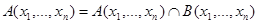
то есть,

.

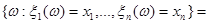
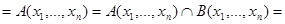
Отсюда следует равенство для вероятностей событий:

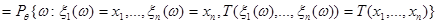
Вероятность справа представим по формуле умножения как произведение условной и безусловной вероятностей:

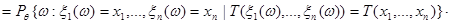
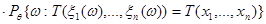
Условная вероятность, есть условное распределение вектора при условии :

.

Поскольку статистика является достаточной для параметра , то функция не зависит от параметра и может зависеть только от ,..., :

.

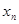Безусловная вероятность очевидно зависит от величины и, возможно, от параметра :

.

Таким образом, для функции правдоподобия получим:

.

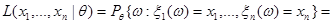
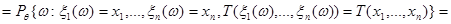
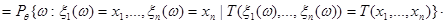
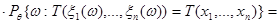
2) Пусть имеет место разложение 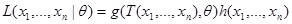, покажем, что в этом случае статистика достаточна для параметра , то есть условная вероятность не зависит от параметра . По определению условной вероятности:

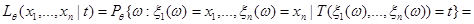
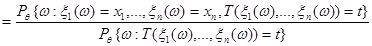
Если , то вероятность, стоящая в числителе равна нулю независимо от значения параметра . В точке :

.

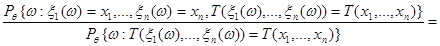
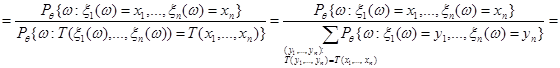
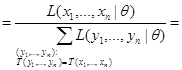
Таким образом,

.

Выражение, стоящее справа, очевидно, не зависит от параметра , поэтому условная вероятность не зависит от параметра , и следовательно статистика достаточна для параметра .

Теорема доказана.