Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 3.6.

Пусть выполнены условия регулярности R1-R5, функция правдоподобия дважды дифференцируема по и

тогда,

.

Доказательство:

При выполнении условий регулярности R1-R5 справедливо соотношение (3.1):

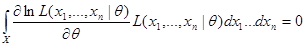
Продифференцировав левую и правую часть по получим:

,

,

,

,

,

,

.

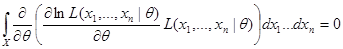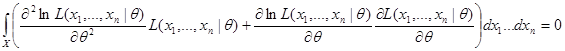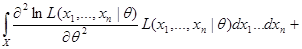
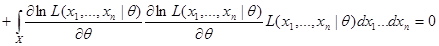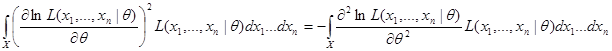Слева от знака равенства располагается информация Фишера , поэтому, окончательно:

.

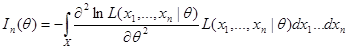Утверждение доказано.

Утверждение 3.7. (аддитивность информации Фишера)

Пусть в наблюдении 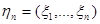случайные величины () совместно независимы и имеют плотности вероятности 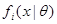соответственно. Если выполнены условия утверждения 3.6, тогда информация Фишера :

,

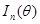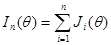где информация Фишера, содержащаяся в наблюдении, образованном одной случайной величиной .

Доказательство:

Поскольку случайные величины () совместно независимы и имеют функции плотности вероятности 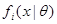(), то функция правдоподобия :

,

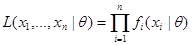тогда,

.

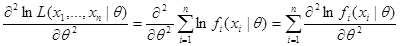В условиях утверждения справедливо утверждение 3.6:

,

откуда

,

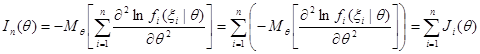где 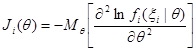- информация Фишера, содержащаяся в наблюдении, образованном одной случайной величиной .

Утверждение доказано.

Утверждение 3.8. (информация Фишера в случае выборки)

Пусть наблюдение 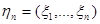является выборкой из распределения с плотностью вероятности 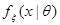. Если выполнены условия утверждения 3.6, тогда информация Фишера

,

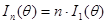где 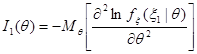– информация Фишера, содержащаяся в наблюдении, образованной случайной величиной, например, .

Доказательство:

В условиях утверждения справедливо утверждение 3.7, согласно которому информация Фишера:

,

.

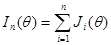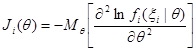Поскольку случайные величины () образуют выборку, то все плотности вероятности одинаковы, 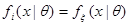, тогда:

,

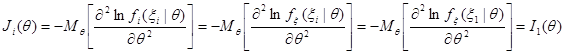и следовательно,

.

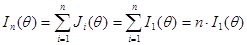Утверждение доказано.