Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 3.10.

Пусть выполняются условия теоремы 3.4, тогда

1) если является эффективной оценкой , то функция правдоподобия имеет вид

,

где , 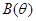и некоторые функции.

2) если функция правдоподобия имеет вид

,

тогда является эффективной оценкой .

Доказательство:

1) Пусть является эффективной оценкой, тогда согласно определению 3.9:

,

где . Согласно следствию 3.5 из этого равенства следует, что:

,

поскольку по определению , то

,

тогда:

.

Предполагая, что существуют интегралы от левой и правой частей, проинтегрируем по :

,

потенцируя получим:

,

где , .

2) Пусть функция правдоподобия 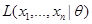имеет вид:

,

логарифмируя и дифференцируя левую и правую часть по , отсюда получим:

,

,

,

,

отсюда в силу следствия 3.5 для дисперсии получим равенство:

,

где 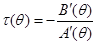, тогда по определению оценка является эффективной.

Утверждение доказано.

Утверждение 3.10 оказывается очень полезным, поскольку в большинстве случаев функция правдоподобия легко выписывается исходя из условий рассматриваемой задачи. Если при этом функция правдоподобия является экспонентной:

,

то при выполнении некоторых условий из утверждения 3.10 непосредственно следует, что 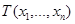является эффективной оценкой величины .

Заметим, что если выполнены условия теоремы 3.4 и существует эффективная оценка для , то существуют эффективные оценки для функций вида , где и действительные числа. Действительно, если эффективная оценка , тогда в силу следствия 3.5:

,

,

где 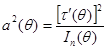. Преобразуя последнее равенство, получим:

,

,

где , , 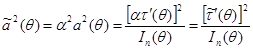. В силу следствия 3.5 отсюда следует, что является эффективной оценкой .