Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Замечание

В многомерном случае неравенство Рао-Крамера формулируется следующим образом: пусть 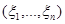– вектор случайных величин, 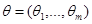– многомерный параметр, 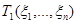, , 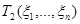…, 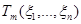– несмещенные оценки 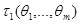, , …, , 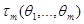тогда при некоторых условиях:

,

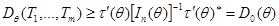(3.5)

где 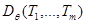– дисперсионная матрица случайных величин 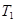, , 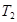…, 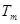(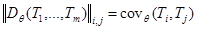), 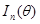– информационная матрица Фишера (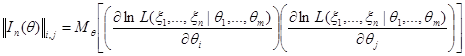), 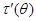– матрица производных (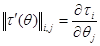), символ 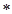означает транспонирование. Неравенство (3.5) следует понимать в следующем смысле: для любого вектора-столбца ,

.

Выражение, стоящее слева, есть квадратичная форма 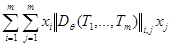, а выражение, стоящее справа, – квадратичная форма :

.

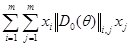Преобразуем выражение, стоящее слева, обозначив вектор-столбец случайных величин и вектор-столбец функций :

.

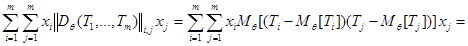
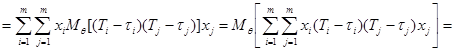
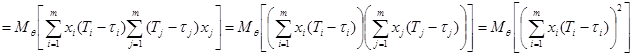Поскольку 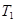, …, 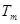несмещенные оценки 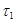, …, , 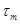то 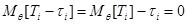, тогда,

.

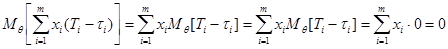Таким образом,

,

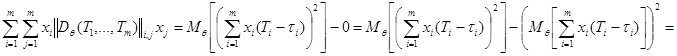
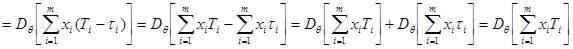поскольку 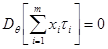, так как 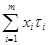– не случайная величина, тогда,

.

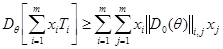Выберем произвольным образом 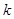, , 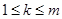и представим, что в векторе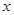 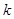-ая компонента равна единице, а все остальные компоненты равны нулю:

,

тогда левая часть неравенства окажется равной 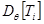, а правая – соответствующему диагональному элементу :

,

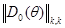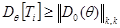Отсюда следует, что диагональные элементы матрицы 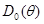являются нижними границами дисперсий оценок , …, .

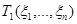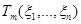Функция правдоподобия, функция вклада и информация Фишера. Свойства информации Фишера в условиях регулярности (вычисление с помощью второй производной, аддитивность в условиях независимости, информация Фишера для выборки). Замечание о характере убывании дисперсии несмещенной оценки, построенной по выборке.