Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача 8.2

Найти решение смешанной задачи для уравнения колебания струны с начальными условиями u(x, 0)=f(x), u_t(x, 0)=Ф(x) (0£ x£ 1, 0£ t£ 0, 01) и краевыми условиями u(0, t)=j(t), u(1, t)=y(x) методом сеток(Δ x=0, 2, Δ t=0, 005). Варианты заданий приведены ниже.

1.		2.		3.
4.		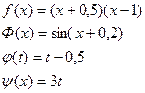5.		6.
7.		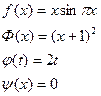8.		9.
10.		11.		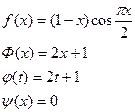12.
13.		14.		15.
16.		17.		18.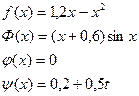
19.		20.

В узлах сетки найти значения функции u(x, t), являющейся решением задачи

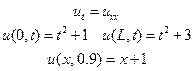
Решение:

Построим сетку по оси Ох с шагом Δ х=0, 2, по оси Оt c шагом Δ t=0, 01.

Точки деления: ; .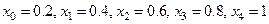

Обозначим . Заменяя в уравнении теплопроводности производные их разностными аналогами, получим следующее разностное уравнение

,

Откуда следует, что

,

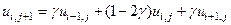где .

Вначале находим значения

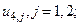
Затем по формуле находим значения решения в остальных точках..

В результате вычислений получим

,

,

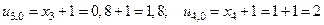
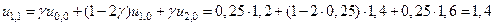
и т.д.

ЗАДАНИЯ К САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ

Вариант 1

1. Решить методом простой итерации и методом Зейделя систему уравнений (решение найти с точностью ):

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х =3.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках: 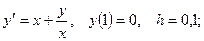найти .

Вариант 2

1. Решить методом простой итерации и методом Зейделя систему уравнений (решение найти с точностью ): .

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

Вычислить значение у для х=9.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

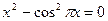4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .

Вариант 3

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью ):

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=15.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти

Вариант 4

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

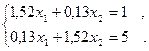
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=0, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

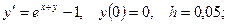найти .

Вариант 5

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

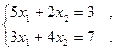
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=2, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: .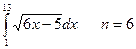

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .

Вариант 6

1. Исследовать сходимость и решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=0, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона. Сравнить полученные значения с точным решением: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .

Вариант 7

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=0, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках: найти .

Вариант 8

1. Исследовать сходимость и решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

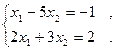
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

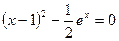4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: .

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .

Вариант 9

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=2, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: .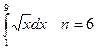

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .

Вариант 10

1. Решить методом простой итерации и методом Зейделя системы уравнений (решение найти с точностью )

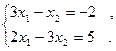
2. Построить интерполяционный многочлен Ньютона по следующей таблице значений функции

.

Вычислить значение у для х=1, 5.

3. Отделить корни уравнения графически и вычислить их, используя метод Ньютона и метод хорд (): .

4. Вычислить интеграл тремя способами: методами прямоугольника, трапеции и Симпсона: .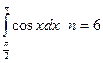

5. Применяя метод Эйлера, найти решение дифференциального уравнения с данными начальными условиями в указанных точках:

найти .