Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения работы. Задача 6.1. Вычислить производную функции в точке с точностью .
|
|
Задача 6.1. Вычислить производную функции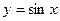 
в точке 
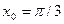с точностью 
.
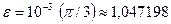Решение:
Положим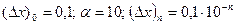 
, откуда: 
.
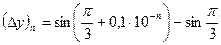Определим приближённое значение производной:
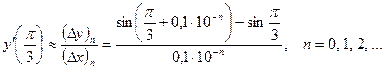
Найдём отношения, аппроксимирующие производную:
.
Заметим, что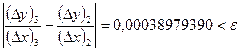 
. Таким образом, начиная с третьего приближения, в соответствии с оценкой (3), получаем искомое приближение производной данной функции с точностью не меньшей заданной. Точное значение 
.
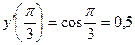Задача 6.2. Вычислить по формуле левых прямоугольников интеграл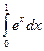 
, разбив отрезок интегрирования на 10 частей. Оценить ошибку вычислений и сравнить полученное значение с точным значением, вычисленным по формуле Ньютона-Лейбница.
Решение.
Вычислим значения подынтегральной функции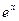 
в точках деления и соответствующие значения занесём в таблицу:
| х | 0, 0 | 0, 1 | 0, 2 | 0, 3 | 0, 4 | 0, 5 | 0, 6 | 0, 7 | 0, 8 | 0, 9 |
| у | 1, 0 | 1, 1051 | 1, 2214 | 1, 3498 | 1, 4928 | 1, 6487 | 1, 8221 | 2, 0137 | 2, 2255 | 2, 4596 |
Воспользуемся формулой (1):
.
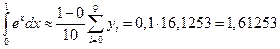Оценим ошибку вычисления. Имеем: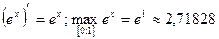 
. Подставляя в формулу 
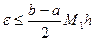, где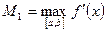 
(наибольшее значение первой производной подынтегральной функции на отрезке интегрирования), получаем 
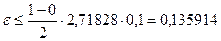. Действительно, сравнивая полученное значение с точным значением, получаем 
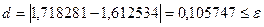. Это весьма значительная ошибка.
ПРАКТИЧЕСКАЯ РАБОТА №7
ТЕМА: «МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ»
Задание:
|
|