Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Пример выполнения работы

Задача 3.1. Решить систему линейных уравнений методом Гаусса

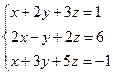
Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

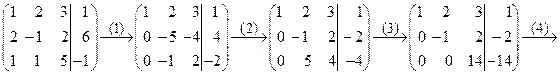
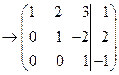
Здесь выполнены следующие элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1.

(2) Вторую строку умножили на –1. Вторую и третью строки поменяли местами.

(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) Вторую строку умножили на –1. Третью строку разделили на 14.

Обратный ход: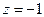

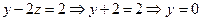
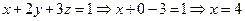
Ответ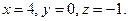

Задача 3.2. Решить систему по формулам Крамера

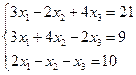
Решение: Решим систему по формулам Крамера

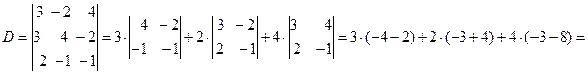
, значит, система имеет единственное решение.

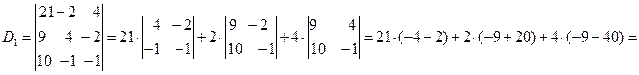
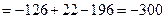
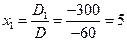
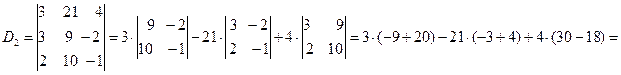
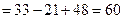
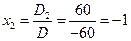
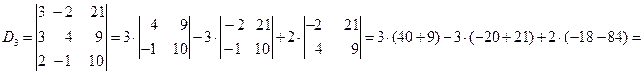
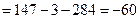
Ответ:

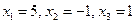
Задача 3.3. Методом Зейделя решить с точностью 0, 01 систему линейных уравнений

,

приведя ее к виду, удобному для итераций.

Приведем систему к виду, в котором элементы главной диагонали превосходили бы остальные элементы строк

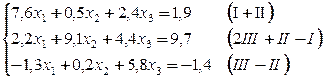
Нулевое приближение .

Первое приближение

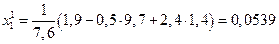
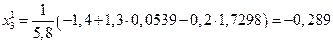
и т.д.

Окончание вычислений определяется условием

,

где - заданное число.

ПРАКТИЧЕСКАЯ РАБОТА №4

ТЕМА: «МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ»