Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 2. Консервативные системы с одной степенью свободы Вопрос 4
|
|
Как известно, консервативные системы - это системы, в которых сохраняется полная колебательная энергия. Одна степень свободы говорит о том, что колебательный процесс описывается одной обобщённой координатой. Понятно, что это некоторая идеализация (абсолютно консервативных систем не существует), однако, возможны системы, которые к ним достаточно близки (высокодобротный колебательный контур, маятник с малым затуханием на хорошем подвесе). В любом случае, тому, что энергия сохраняется, отвечают, например, колебательные системы, которые описываются уравнениями вида (1.36) при условии, что правая часть зависит от обобщённых координат, но не от обобщённых скоростей, т. е. 
(здесь все множители нормированы на единицу массы). Тогда выражение для кинетической энергии должно иметь вид:
,
где 
(обобщённая скорость). Так как потенциальная сила есть производная потенциальной величины по обобщённой координате, тогда сама потенциальная энергия есть интеграл
| (2.1) |
(здесь в положении q 0 просто ставится ноль потенциальной энергии).
Ниже следуют примеры консервативных систем.
1. Груз массы m на пружине жёсткостью k. Его колебания описываются уравнением 
, где 
.
2. Резонансный LC-контур без сопротивления: 
, где q - заряд на пластинах конденсатора.
3. Математический маятник длиной l: 
, 
.
|
|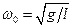