Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вопрос 37

Производная сложной функции

Если функция f имеет производную в точке х₀, а функция g имеет производную в точке y₀=f(x₀)y то сложная функция h(х) = g(f(х)) также имеет производную в точке х₀, причем

h’(x₀) = g’(f(x₀))•f’(x₀) (1)

Для доказательства формулы (1) надо (как и раньше) при Δ x≠ 0 рассмотреть дробь Δ h/Δ x и установить, что

при Δ x→ 0. Введем обозначения:

Δ y = f(x₀+Δ x)-f(x₀)= Δ f

Тогда Δ h = h(х₀ + Δ х) - h(x₀) = g(f(x₀ +Δ x)) - g(f(x₀)) = g(y₀ + Δ y) - g(y₀) = Δ g.

Δ y→ 0 при Δ x→ 0, так как f дифференцируема в точке x₀.

Далее доказательство мы проведем только для таких функций f, у которых Δ f≠ 0 в некоторой окрестности точки х₀. Тогда

при Δ x→ 0, так как Δ f/Δ x→ f’(x₀) при Δ x→ 0, а Δ g/Δ y→ g’(y₀) при Δ y→ 0, что выполнено при Δ x→ 0.

15.Обратная матрица. Алгоритм её решения.

1. Обратная матрица.

Если определитель квадратной матрицы А равен нулю, то матрица называется особенной или вырожденной.

Если определитель квадратной матрицы А неравен нулю, то матрица называется неособенной или невырожденной.

Матрица А^-1 называется обратной для квадратной невырожденнойматрицы А, если произведение А× А^-1=Е или А^-1× А=Е, где Е - единичная матрица.

Найдем конкретный вид обратной матрицы:

1. Заменим в квадратной невырожденнойматрице А каждый элемент его алгебраическим дополнением a_ij®A_ij.

2. Протранспонируем полученную матрицу А_ij®A_ji®A_c® .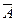

Матрица 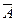называется союзной (присоединенной) для матрицы А.

3. Разделим полученную союзную матрицу на определитель .

.

Докажем, что формула дает нам обратную матрицу. Для этого составим произведение А× А^-1=С. С=Е