
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Парабола
|
|
Определение- множество точек плоскости, каждая из которых
равно удалена от данной точки F, называемой фокусом,
и данной прямой называемой директрисой-парабола.
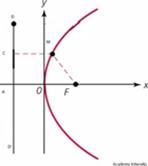
Используем определение и получим ур-е параболы:
Через данную точку F проведем прямую перпендикулярную в данной
Директрисе DD’ и направленной от директрисы к фокусу. Примем эту прямую
За ось Ox. Расстояние от директрисы до фокуса равно P (AF=P, P> 0).
P-параметр параболы. Середину отрезка A примем за начало координат
и проведем через эту точку ось Oy. Фокус имеет координаты F(P/2; 0).
Берем произвольную точку M(x, y) и опускаем перпендикуляр на директрису, т.е
Будет иметь координаты С(-p/2; y). По определению параболы MC=MF
Найдем расстояние между точками М(x, y) и С(-p/2; y); M(x, y) и F(p/2; 0)/
Учитываем определение 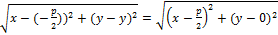 -
-
уравнение параболы. Возведем обе части в квадрат
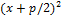 =
= 
Окончательно получаем
 , т.к оно второй степени.,
, т.к оно второй степени.,
то это кривая второго порядка.
|
|
