Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Уравнение плоскости, проходящее через данную точку

Положение плоскости в декартовой системе координат определяется заданной точкой на плоскости и ненулевым вектором, перпендикулярным плоскости.

Пусть на плоскости дана точка М₀(х₀, у₀, z₀), и известен вектор перпендикулярный плосткости (A, B, C). Берём на плоскости произвольную точку М(х, у, z). Вектор лежит в плоскости. Следует векторы и перпендикулярны, т.е выполняется равенство: и * =0

(скалярное произведение векторов).

= -

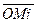
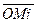( - )=0

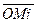= (х₀, у₀, z₀), =(х, у, z).

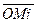( - )= (х- х₀, у- у₀, z- z₀₎

Условие перпендикулярности двух векторов: A(x – x₀) + B(y – y₀) + C(z – z₀) = 0. Это уравнение плоскости, проходящей через т. М₀(х₀, у₀, z_{0) и перпендикулярной вектору} (A, B, C)

Преобразуем это уравнение, раскрыв скобки

Ax + By + Cz + (- Axо – Byо – Сzo) =0

Введём обозначение D= -Axо – Byо – Сzo

В результате получаем Ax + By + Cz+D =0 это Общее уравнение плоскости

Вопрос 10. Угол между двумя плоскостями Условия параллельности и перпендикулярности плоскостей (10)

Пусть даны 2 непересекающиеся плоскости:

А1х+В1у+С1t+D1=0 (1)

A2x+B2y+C2t+D2=0 (2)

Угол между плоскостями равен углу ℓ (фи),

Между векторами ň 1(A1? B1? C1) ň 2(A2, B2, C2)

И определяется по формуле:

cos ℓ (фи)= A1A2+B1B2+C1C2

Если ℓ (фи)=П/2, то получ равенство:

А1А2+В1В2+С1С2=0

Формула следует из условия перпендикулярных векторов ň 1 и ň 2.

Если плоскости 1 и 2 параллельны, то вектора будут КОЛАНЕАРНЫМИ (одинак направление но разная длина)

А1/А2=В1/В2=С1/С2 (условие параллельности двух плоскостей)

А1/А2=В1/В2=С1/С2=Д1/Д2 (плоскости совпадают)