Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос 18.
|
|
Векторное пространство, математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства.
ОпределениеВекторное пространство Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям: 1) х + у = у + х (перестановочность сложения);
2)(х + у)+ z = x +(y + z) (ассоциативность сложения);
3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x;
4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,
5) 1*х=х
6) a (bx)=(ab) х (ассоциативность умножения);
7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя);
8) a (х + у)= aх + aу (распределительное свойство относительно векторного множителя).
Совокупность всех n-мерных векторов, рассматриваемая с определенными вней операциями сложения и умножения на число, подчиняющимся пунктам 1-8, называется n-мерным линейным векторным пространством. Если координаты векторов – вещественные числа, то пространство называют арифметическим и обозначают R в степени n.
Ненулевые векторы а и b коллинеарны тогда и только тогда, когда вектор b = α ā, где α ≠ 0. Это означает, что у коллинеарных векторов их одноименные координаты пропорциональны: а1/b1=…= a n-ное/ b n-ное = α
Вопрос № 20: свойства линейной зависимости
Теорема 1: если система векторов ā 1, ā 2…, ā n содержит вектор, то она линейно зависима
Теорема 2: если часть системы линейно зависима, то и вся система линейно зависима
Теорема 3: диагональная система линейно независима
Доказательство: согласно определению (метод Гауса: решения уравнений могут быть использованы для выявления линейной зависимости m-мерных векторов), теорема будет доказана, если мы установим, что равенство:
λ 1ā 1+ λ 2ā 2+ λ Rā R=0
это равенство имеет место лишь при условии
λ 1=λ 2=…=λ R=0
т.к. равенство
b‾ 1 = (b11, b12…b1R..b1n)
b‾ 2 = (, b22…b2R..b2n)
b‾ R =(0, …0…bRR…bRn) означает равенство из одноименных координат, то вместо одного векторного уровня (λ 1ā 1+ λ 2ā 2+ λ Rā R=0) можно записать систему n-линейных уравнений
λ 1*β 11=0
λ 1*β 12 + λ 2β 22 = 0
λ 1*β 1R + λ 2β 2R +…+ λ R*β RR = 0
…..
λ 1*β 1m + λ 2β 2m +λ R+ λ R*β Rm = 0
т.к. b11 ≠ 0 (по условию), то из первого уравнения системы получаем, что λ 1=0, тогда второе уравнение системы принимает вид λ 2β 2=0, т.к. b2=0
получаем, что λ 1=0, тогда из R-ого уравнения получаем, что λ R=0, равенство λ 1ā 1+ λ 2ā 2+ λ Rā R=0 возможно только тогда, когда все коэффициенты =0
теорема 4: любой вектор ā принадлежит Rn может быть представлен единственным образом в виде линейной комбинации единичных векторов.
Доказательство: пусть вектор ā =(λ 1, λ 2…λ R) его можно представить так:
ā =(λ 1, 0…0) + (0, λ 2…0)+..+(0, 0…λ n)=λ 1(1; 0, …0) + λ 2 (0, 1, 1…0)…+λ n (0,..0, 1)
вынести компоненты
λ 1ē 1 + λ 2ē 2+…+ λ nē n
т.о. ā = λ 1ē 1 + λ 2ē 2+…+ λ nē n
докажем единственность разложения
предположим, что существует другое разложение вектора по единичным векторам
ā = λ 1ē 1 + λ 2ē 2+…+ λ nē n
вычтем предыдущие выражения
Ō = (λ 1-λ 1ʹ) ē 1 + (λ 2-λ 2ʹ)ē 2…+(λ n-λ nʹ)ē n
Система векторов ē, ē 2…ē n линейно независима. Следовательно предыдущее равенство имеет место в случае, когда
λ 1-λ 1ʹ =0
λ 2-λ 2ʹ =0
λ n-λ nʹ =0
т.е. при условии λ 1 = λ 1ʹ, λ 2=λ 2ʹ …λ n=λ nʹ
теорема 5: в пространстве Rn любая система состоящая более чем из n векторов линейно зависима R2
ā 1=(2, 1)
ā 2=(3, 2)
ā 3=(2, 4)
Вопрос 4
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M1(x1, y1, z1) и M2(x2, y2, z2), тогда уравнение прямой, проходящей через эти точки: 
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.
На плоскости записанное выше уравнение прямой упрощается: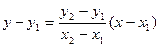 
, если х1 ¹ х2 и х = х1, если х1 = х2.
Дробь 
= k называется угловым коэффициентом прямой.
Уравнение прямой на плоскости
Определение. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.
|
|