Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Линейные дифференциальные уравнения первого порядка. Метод вариации постоянной для решения линейного дифференциального уравнения первого порядка.

Определение линейного уравнения первого порядка

Дифференциальное уравнение вида

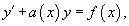
где a(x) и b(x) − непрерывные функции x, называтся линейным неоднородным дифференциальным уравнением первого порядка.

Метод вариации постоянной

Сначала необходимо найти общее решение однородного уравнения:

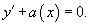
Общее решение однородного уравнения содержит постоянную интегрирования C. Далее мы заменяем константу C на некоторую (пока еще неизвестную) функцию C(x). Подставляя это решение в неоднородное дифференциальное уравнение, можно определить функцию C(x).

Описанный алгоритм называется методом вариации постоянной. Разумеется, оба метода приводят к одинаковому результату.

Решить дифференциальное уравнение .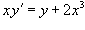

Solution.

Будем решать данную задачу методом вариации постоянной. Сначала найдем общее решение однородного уравнения:

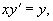
которое решается разделением переменных:

где C − произвольное положительное число.

Теперь заменим константу C на некоторую (пока неизвестную) функцию C(x) и далее будем искать решение исходного неоднородного уравнения в виде:

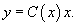
Производная равна

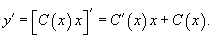
Подставляя это в дифференциальное уравнение, получаем:

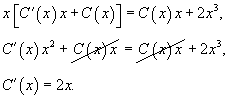
Интегрируя, находим функцию C(x):

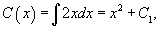
где C1 − произвольное действительное число.

Таким образом, общее решение заданного уравнения записывается в виде:
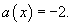