Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Ряды Фурье для четных и нечетных функций.

Функция y=f(x) называется четной, если выполнено условие:

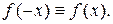
График четной функции симметричен относительно оси Oy. Например, функция 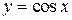- четная.

Функция y=f(x) называется нечетной, если выполнено условие:

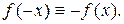
График нечетной функции симметричен относительно начала координат. Например, функция 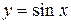- нечетная.

Теорема. Если функция y=f(x) четная с периодом T=2p, то

(1)

Доказательство

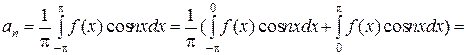
Функция y=f(x)cos nx четная. Введем для первого интеграла замену:

Аналогично, функция y=f(x)sin nx нечетная. С помощью той же замены получим:

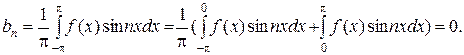
Можно сформулировать это правило так: четная периодическая функция разлагается в ряд по четным гармоническим функциям, нечетная функция по нечетным.

Теорема. Если функция y=f(x) нечетная с периодом T=2p, то

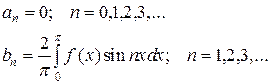(2)

Доказательство проводится аналогично. Разобрать самостоятельно. Можно сформулировать это правило так: четная периодическая функция разлагается в ряд по четным гармоническим функциям, нечетная функция по нечетным.

Пример. Найти разложение в ряд Фурье функции 2p- периодической функции, которая равна y=x на (-p, p). Изобразим график функции

Так как функция нечетная, то an=0. Коэффициенты

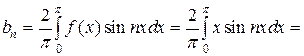
Применим для вычисления формулу интегрирования по частям

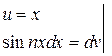
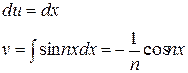
Получаем

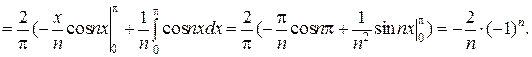
Разложение имеет вид
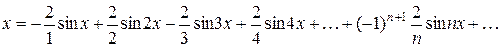