Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрические ряды Фурье. Нахождение коэффициентов ряда Фурье.
|
|
Тригонометрический ряд Фурье — представление произвольной функции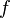 
с периодом 
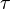в виде ряда
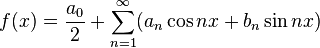
| (1) |
или используя комплексную запись, в виде ряда:
.
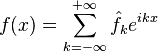Тригонометрическим рядом Фурье функции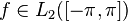 
называют функциональный ряд вида
|
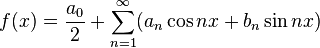
| (1) |
где
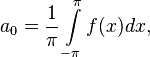
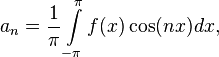
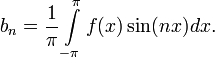
Числа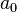 
, 
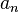и 
(
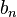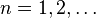) называются коэффициентами Фурье функции 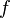. Формулы для них можно объяснить следующим образом. Предположим, мы хотим представить функцию 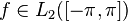в виде ряда (1), и нам надо определить неизвестные коэффициенты 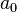, 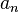и 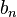. Если умножить правую часть (1) на 
и проинтегрировать по промежутку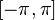 
, благодаря ортогональности в правой части все слагаемые обратятся в нуль, кроме одного. Из полученного равенства легко выражается коэффициент 
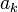. Аналогично для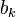 
Ряд (1) сходится к функции 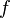в пространстве 
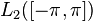. Иными словами, если обозначить через 
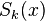частичные суммы ряда (1):
,
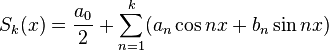то их среднеквадратичное отклонение от функции 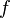будет стремиться к нулю:
.
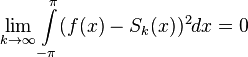Несмотря на среднеквадратичную сходимость, ряд Фурье функции, вообще говоря, не обязан сходиться к ней поточечно(см.ниже).
|
|