Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Метод неопределенных коэффициентов для решения неоднородных дифференциальных уравнений высших порядков. Специальный вид правой части.

Если правая часть f(x) дифференциального уравнения представляет собой функцию вида

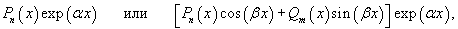
где Pn(x), Qm(x) − многочлены степени n и m, соответственно, то для построения частного решения можно использовать метод неопределенных коэффициентов.

В этом случае мы ищем частное решение в форме, соответствующей структуре правой части уравнения. Так, например, для функции

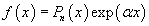
частное решение имеет вид

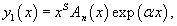
где An(x) − многочлен той же степени n, как и Pn(x). Коэффициенты многочлена An(x) определяются прямой подстановкой пробного решения y1(x) в неоднородное дифференциальное уравнение.

В так называемом резонансном случае, когда число α в показательной функции совпадает с корнем характеристического уравнения, в частном решении появляется дополнительный множитель xs, где s равно кратности корня. В нерезонансном случае полагают s = 0.

Такой же алгоритм применяется, когда правая часть уравнения задана в виде

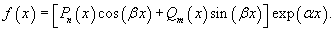
Здесь частное решение имеет аналогичную структуру и записывается как

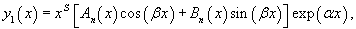
где An(x), Bn(x) − многочлены степени n (при n ≥ m), а степень s в дополнительном множителе xs равна кратности комплексного корня α ± β i в резонансном случае (т.е. при совпадении чисел α и β с комплексным корнем характеристического уравнения), и, соответственно, s = 0 в нерезонансном случае.

Решить дифференциальное уравнение yIV − y = 2cos(x).

Решение.

Сначала рассмотрим однородное уравнение

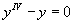
и построим его общее решение. Характеристическое уравнение

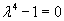
имеет следующие корни:

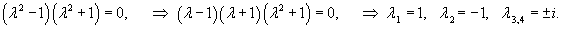
Следовательно, общее решение однородного уравнения имеет вид:

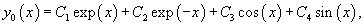
где C1,..., C4 − произвольные числа.

Теперь найдем частное решение неоднородного уравнения. Здесь мы имеем резонансный случай, поскольку выражение в правой части соответствует по структуре комплексному корню α ± iβ = ±i. Поэтому будем искать частное решение в виде

Производные этой функции равны:

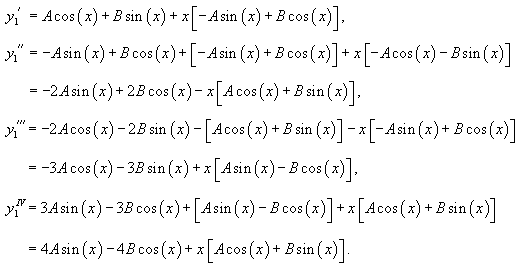
Подставляем найденные производные в неоднородное уравнение и определяем коэффициенты A, B:

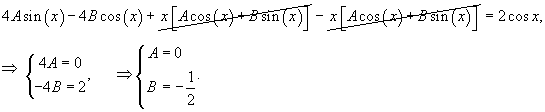
Итак, частное решение выражается в виде

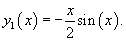
Тогда общее решение исходного неоднородного уравнения записывается как
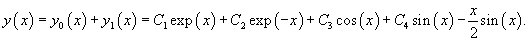