Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Степенные ряды. Теорема Абеля. Область сходимости степенного ряда.

Определение. Степенным рядом называется функциональный ряд вида:

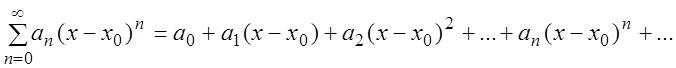, (3.5)

где – постоянные числа, называемые коэффициентами ряда (3.5), 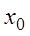– фиксированное число.

При получаем степенной ряд вида:

(3.6)

Очевидно, что для (3.5) число является точкой сходимости.

Выясним вопрос об области сходимости степенного ряда.

Теорема 3.1 (теорема Абеля)

1) Если степенной ряд (3.6) сходится при некотором значении 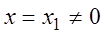, то он абсолютно сходится при всяком значении 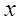, удовлетворяющим условию: .

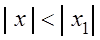2) Если степенной ряд (3.5) расходится при некотором значении 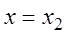, то он расходится при любых 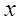, для которых .

Доказательство

1) Так как по условию числовой ряд сходится, то его общий член при , откуда следует, что числовая последовательность

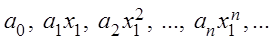
ограничена, т.е. существует число такое, что

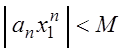, (3.7)

Перепишем ряд (3.6) в виде:

(3.8)

и рассмотрим ряд, составленный из абсолютных величин его членов:

(3.9)

Члены ряда (3.9) в силу неравенства (3.7) меньше соответствующих членов ряда

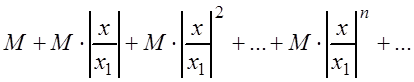(3.10)

При 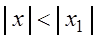ряд (3.10) представляет собой геометрическую прогрессию со знаменателем 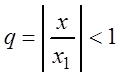и, следовательно, сходится. Так как члены ряда (3.9) меньше соответствующих членов ряда (3.10), то по признаку сравнения (см. теорему 2.3) ряд (3.9) также сходится, а это значит, что ряд (3.6) при 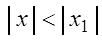сходится абсолютно (см. теорему 2.8).

2) Докажем теперь вторую часть теоремы. По условию в точке 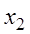ряд (3.6) расходится. Требуется показать, что он расходится для всех 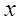, удовлетворяющих условию: . Предположим обратное, т.е. допустим, что при некотором значении 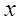таком, что , ряд (3.6) сходится. Тогда, по только что доказанной первой части теоремы, ряд (3.6) должен сходится и в точке 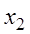, так как . Но это противоречит тому, что в точке 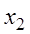ряд расходится. Следовательно, ряд расходится и в точке 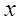. Таким образом, теорема полностью доказана.

Теорема Абеля утверждает, что если 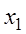– точка сходимости степенного ряда, то во всех точках, расположенных на интервале , этот ряд сходится абсолютно (рис. 3.1, а), а если 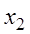– точка расходимости степенного ряда (3.6), то во всех точках, расположенных вне интервала , ряд расходится (рис. 3.1, б).

Из этого можно заключить, что существует такое число 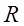, что при 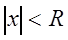мы имеем точки абсолютной сходимости и при 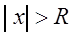– точки расходимости.

Таким образом, имеет место следующая теорема о строении области сходимости степенного ряда (3.6).

Теорема 3.2. Областью сходимости степенного ряда (3.6) является интервал с центром в начале координат.

Определение. Неотрицательное число 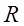, такое, что при всех степенной ряд (3.6) сходится, а при всех – расходится, называется радиусом сходимости степенного ряда (рис. 3.2). Интервал 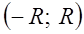называется интервалом сходимости степенного ряда (3.6).

На концах интервала (т.е. при и при ) вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.

Если ряд (3.6) сходится только в одной точке , то для него радиус сходимости . Если ряд (3.6) сходится для любого действительного числа 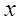, то будем считать, что .

Радиус сходимости степенного ряда обычно находится с использованием признаков Даламбера и Коши.