
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функциональные ряды. Область сходимости. Понятия абсолютной и равномерной сходимости функционального ряда.
|
|
Определение. Пусть 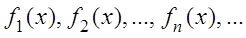 – бесконечная последовательность функций, определённых на некотором множестве
– бесконечная последовательность функций, определённых на некотором множестве 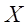 . Выражение вида:
. Выражение вида:
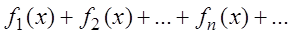 (3.1)
(3.1)
называется функциональным рядом и обозначается сокращённо: 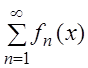 .
.
Пусть число 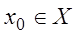 , тогда ряд:
, тогда ряд:
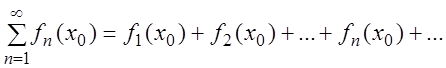 (3.2)
(3.2)
является числовым рядом.
Определение. Если числовой ряд (3.2) сходится, то ряд (3.1) называется сходящимся в точке х0, а число 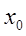 называется точкой сходимости функционального ряда (3.1).
называется точкой сходимости функционального ряда (3.1).
Определение. Множество 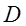 всех точек сходимости функционального ряда (3.1) называется его областью сходимости.
всех точек сходимости функционального ряда (3.1) называется его областью сходимости.
Последнее определение можно сформулировать иначе: областью сходимости функционального ряда называется совокупность значений 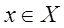 , при которых ряд (3.1) сходится. Как правило, область сходимости
, при которых ряд (3.1) сходится. Как правило, область сходимости 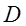 не совпадает с областью определения
не совпадает с областью определения 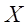 функционального ряда, а является её частью, т.е.
функционального ряда, а является её частью, т.е. 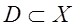 .
.
Пример 1. Найти область определения и область сходимости функционального ряда:
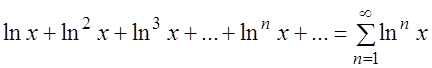 .
.
Решение. Так как ряд составлен из функций вида 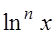 , то их областью определения является область определения основной элементарной функции
, то их областью определения является область определения основной элементарной функции 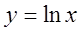 , т.е.
, т.е. 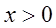 . Кроме того, данный ряд является суммой членов геометрической прогрессии с первым членом
. Кроме того, данный ряд является суммой членов геометрической прогрессии с первым членом 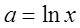 и знаменателем
и знаменателем 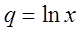 . Такой ряд сходится, если
. Такой ряд сходится, если 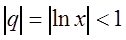 , т.е. при
, т.е. при
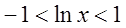 ,
, 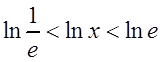 .
.
Поэтому областью сходимости является интервал 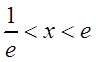 .
.
Таким образом, 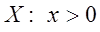 и
и 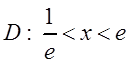 . Очевидно, что
. Очевидно, что 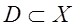 .
.
Определение. Функция 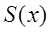 называется суммой ряда (3.1) в некоторой области
называется суммой ряда (3.1) в некоторой области 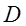 , если для любого
, если для любого 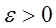 существует такой номер
существует такой номер 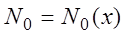 , что при всех
, что при всех 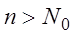 справедливо неравенство:
справедливо неравенство:
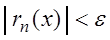
 . (3.3)
. (3.3)
В общем случае 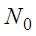 зависит от
зависит от 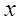 , т.е. при заданном
, т.е. при заданном 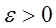 натуральные числа
натуральные числа 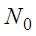 различны для различных значений
различны для различных значений 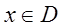 . Если же существует один номер
. Если же существует один номер 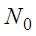 , такой, что при
, такой, что при 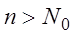 неравенство (3.3) справедливо для всех
неравенство (3.3) справедливо для всех 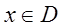 , то ряд (3.1) называется равномерно сходящимся в D.
, то ряд (3.1) называется равномерно сходящимся в D.
В случае равномерной сходимости функционального ряда его n-я частичная сумма является приближением суммы ряда с одной и той же точностью для всех 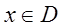 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Определение. Функциональный ряд (3.1) называется мажорируемым в некоторой области 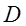 , если существует сходящийся числовой ряд:
, если существует сходящийся числовой ряд:
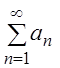
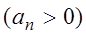 , (3.4)
, (3.4)
такой, что для всех 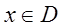 справедливы неравенства:
справедливы неравенства: 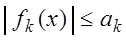
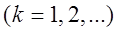 .
.
Ряд (3.4) называется мажорантным (мажорирующим) рядом.
Мажорируемый ряд является рядом равномерно сходящимся.
Например, функциональный ряд:
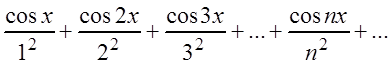
мажорируется рядом 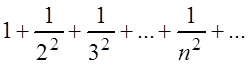 , так как
, так как  . Данный функциональный ряд равномерно сходится на всей оси
. Данный функциональный ряд равномерно сходится на всей оси  , поскольку он мажорируется при любом
, поскольку он мажорируется при любом 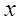 .
.
Равномерно сходящиеся ряды обладают некоторыми общими свойствами:
1) если члены равномерно сходящегося ряда непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке;
2) если члены ряда (3.1) непрерывны на отрезке 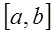 и ряд равномерно сходится на этом отрезке, то в случае, когда
и ряд равномерно сходится на этом отрезке, то в случае, когда 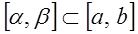 ,
,
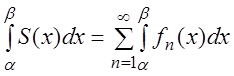 ,
,
где 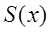 – сумма ряда (3.1);
– сумма ряда (3.1);
3) если ряд (3.1), составленный из функций, имеющих непрерывные производные на отрезке 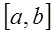 , сходится на этом отрезке к сумме
, сходится на этом отрезке к сумме 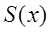 и ряд
и ряд
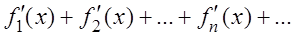
равномерно сходится на том же отрезке, то 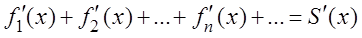 .
.
Последние два свойства определяют условия, при которых функциональные ряды можно почленно интегрировать и дифференцировать.
|
|
