Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Знакочередующиеся ряды. Теорема Лейбница.

Рассмотрим важный класс рядов, называемый знакочередующимися.

Определение.Знакочередующимся рядомназывается ряд вида

u1 – u2 + u3 - u4 +…+(-1) 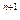un +...,

где u1, u2, u3..., - положительные для всех 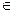n N.

ТЕОРЕМА (ПРИЗНАК ЛЕЙБНИЦА). Знакочередующийся ряд

u1 – u2 + u3 - u4 +… (un> 0), (4.1)

сходится, еслипоследовательность абсолютных величин членов ряда монотонно убывает, т.е. u1> u2> u3> … (4.2)

и если 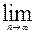un=0 (4.3)

при этом сумма S ряда(4.1) удовлетворяет неравенствам 0< S < u1.

Для остатка ряда 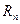в этом случае справедлива оценка .

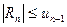ПРИМЕР.Исследовать сходимость ряда:

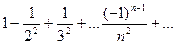
Имеем: 1> 1/4> 1/9>...– члены ряда монотонно убывают и 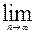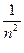=0.

По Теореме Лейбница ряд сходится.

Замечание: В Т.Лейбница важны как условие 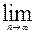un=0, так и u1> u2> u3>...

Например, для ряда 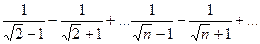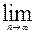un=0, но условие

1/ 0, 41> 1/2, 41 > 1/1, 73 > 1/2, 73... или

2, 44> 0, 41> 0, 58> 0, 37... неверно и ряд расходится.

ПРИМЕР.Вычислить приблизительно сумму ряда .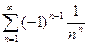

Имеем знакочередующийся ряд, сходится.Возьмем пять элементов этого ряда:

,

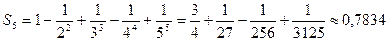Вычислим ошибку: 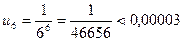; итак, .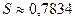