Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Состояние продуктов синтеза системы Ti-C-Ni

В разд. 1 было показано, что при температурах СВС-прессования деформирование продуктов синтеза происходит по механизму вязкого течения вещества твердой фазы. Континуальная теория вязкого течения сжимаемых тел, в наиболее общем виде учитывающая реологические свойства вещества, изложена в работах [186, 188, 230]. Особенности континуальной теории неупругого деформирования порошковых тел с дискретной структурой и контактным взаимодействием частиц была рассмотрена в разд. 3. Для удобства дальнейшего изложения кратко напомним основные положения этой теории.

Определяющая зависимость между тензором напряжений s_ij и тензором скоростей е_ij для пористого тела с произвольным законом вязкого течения твердой фазы имеет вид [188, 230]

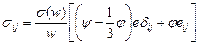, (4.1)

где w – эквивалентная скорость деформации твердой фазы; s(w) – эквивалентное напряжение; e – скорость изменения объема; d _ij – символ Кронекера; y, j – функции относительной плотности r. В настоящей работе эти функции принимаются равными

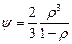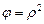; . (4.2)

Для вязких порошковых тел эквивалентная скорость деформации твердой фазы w выражается через инварианты макроскопического тензора скоростей деформаций:

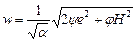, (4.3)

где a – объемная доля вязкодеформируемой твердой фазы; H – интенсивность скоростей деформации сдвига. Параметр a отражает неоднородный характер деформации частиц твердой фазы и бесконечно малое сопротивление порошкового тела в состоянии насыпной плотности. Зависимость a (r) для монодисперсных сферических частиц имеет вид

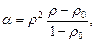(4.4)

где r ₀ – насыпная плотность.

Закон вязкого течения твердой фазы содержится в зависимости между эквивалентной скоростью деформации w и эквивалентным напряжением s (w). Для линейно-вязкой твердой фазы эквивалентная скорость деформации w и эквивалентное напряжения s (w) связаны зависимостью [188]

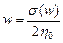, (4.5)

где h ₀ – коэффициент сдвиговой вязкости твердой фазы. Для нелинейно-вязких тел, к которым относятся тугоплавкие соединения, и в частности карбид титана, наиболее часто используется степенной закон течения Оствальда-де Виля:

. (4.6)

Коэффициент 1/2 в (4.6) выбран из условия предельного перехода при n = 1, когда A ^-1 = h ₀. Именно для степенного закона течения в научной литературе накоплен обширный теоретический и экспериментальный материал по характеристикам ползучести тугоплавких соединений [82].

Из (4.1) с учетом зависимостей (4.3) и (4.6) получаем определяющие соотношения для нелинейно-вязкого дисперсного тела:

. (4.7)

Реологические свойства вещества твердой фазы и их зависимость от температуры учитываются параметром А [82]:

, (4.8)

где Т – абсолютная температура; U – энергия активации; k – постоянная Больцмана; С – константа. Экспериментальные значения этих параметров получены в работе [82] при горячем изотермическом прессовании порошка карбида TiC в жесткой матрице с учетом сил внешнего трения. При выводе аналитического уравнения использовался коэффициент объемной вязкости z линейного тела:

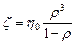. (4.9)

В нашем случае функция y вида (4.2) приводит к выражению

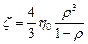(4.10)

и отличается от коэффициента z, используемого в работе [82], множителем 4/3. Из аналитического уравнения прессования [82] получено, что параметр А из (4.8) будет связан с экспериментальной величиной А ₁ [82] соотношением

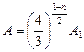. (4.11)

Для порошкового карбида титана TiC реологические константы нелинейно-вязкого течения с учетом принятой формы функции y (r) имеют следующие значения: энергия активации U = 8, 42× 10^-19 Дж; предэкспонента С = 9× 10^-34 м⁷× Н^-2/c; показатель нелинейности n = 3.

Рассмотрим более подробно связь определяющих уравнений с физическим состоянием продуктов синтеза системы Ti-C-Ni. Особенностью физического состояния сплавов TiC-Ni, синтезированных в режиме горения, является то, что они в широком температурном диапазоне содержат жидкую фазу – карбидоникелевый расплав. В разд. 3 показано, что при уровне напряжений, характерных для процессов обработки давлением, для твердожидких материалов можно использовать приближение идеальной жидкости. В этой модели сопротивление деформации оказывает только твердая фаза, и структурным параметром, контролирующим механическое поведение твердожидкого тела, является объемная доля твердой фазы r_S. Соответственно параметры y, j и a будут функционально связаны с объемом твердой фазы:

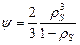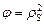; ; . (4.12)

Объемная доля твердой фазы r_S в пористом твердожидком теле с относительной плотностью r рассчитывается по зависимости

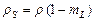, (4.13)

где m_L – объемная доля жидкой фазы в компактном материале. Величина m_L определяется по диаграмме состояния системы TiC-Ni. Для расчета относительной плотности r продуктов синтеза используется модель наследования синтезированной заготовкой размеров шихтовой заготовки. Методика расчета начальной плотности продуктов синтеза в рамках этой модели была рассмотрена в разд. 2. В табл. 4.1 приведены расчетные значения характеристик плотности и фазового состава для сплавов системы TiC-Ni при температуре горения T _г.

Объемная доля твердой фазы r _S определяет механическую устойчивость и сопротивление деформации дисперсного тела. В нормальных условиях начальная плотность механически устойчивой дисперсной среды не может быть меньше насыпной плотности r _н. Соответственно механическую устойчивость дисперсного твердожидкого тела определяет насыпная плотность твердой фазы r_{S H}.

Т а б л и ц а 4.1