Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Частное условие пластичности

Условие пластичности порошковых материалов (3.64) содержит ряд эмпирических параметров. Это насыпная относительная плотность r ₀, напряжение s ^*, константа сцепления K ₀, коэффициент внутреннего трения f, предельное напряжение t ₀ и эмпирическая константа b в выражении (3.65) для объемной доли твердой фазы a. Насыпная относительная плотность r ₀ определяется взвешиванием. Остальные параметры находятся по результатам механических испытаний следующим образом.

Напомним, что эллиптическое условие пластичности эквивалентно критерию пластичности Бельтрами: пластическое течение наступает тогда, когда сумма удельной упругой энергии изменения объема и формы несплошного тела достигает своего предельного значения. Функции пористости y и j представляют собой соответственно отношения эффективных модулей объемного сжатия К и сдвига m порошкового тела к модулю сдвига его вещества m ₀:

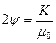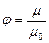; . (3.78)

Тогда левая часть эллиптического условия пластичности будет характеризовать полную энергию упругого деформирования u порошкового тела на поверхности нагружения, приведенную к модулю сдвига m ₀:

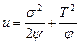. (3.79)

Для функций y и j принимаются зависимости, полученные В.В. Скороходом:

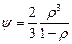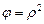; . (3.80)

При известных функциях y и j сначала находится экспериментальная зависимость полной упругой энергии порошкового тела от относительной плотности u (r). Для этого проводятся механические испытания с измерением компонентов напряженного состояния и последующим расчетом среднего напряжения s и интенсивности касательных напряжений Т. Затем при соответствующей обработке зависимости u (r) находятся искомые эмпирические параметры.

Так как находится энергетическая характеристика u (r), то отсутствуют жесткие требования к схеме проведения механических испытаний, поэтому в настоящей работе феноменологические параметры условия пластичности для сыпучих материалов оболочки определялись при одностороннем прессовании в закрытой матрице [206].

При прессовании в закрытой матрице измерялись полное давление прессования q и радиальное давление р_r. Кроме того, для расчета плотности определялась текущая высота спрессованного объема. Для исключения влияния внешнего трения на величину истинного осевого давления использовали известную методику [132]. Суть ее заключается в том, что в одной матрице спрессовываются два образца одинаковой плотности, но имеющие разные массы и боковые площади трения. Истинное осевое давление р_z, соответствующее текущей плотности, рассчитывается по зависимости

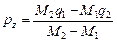, (3.81)

где М ₁, М ₂ – массы навесок; q ₁, q ₂ – полные давления прессования навесок.

Прессование проводили в цилиндрической матрице радиусом 39 мм на гидропрессе Д-1932 с номинальным усилием 1600 кН. Песок перед прессованием просеивали через сито с диаметром ячейки 1, 0 мм. Кроме песка исследовали шамотную крошку и смесь песка с шамотной крошкой в соотношении 3: 1 (по объему). Измерение полного q и радиального р_r давлений осуществляли тензометрическим методом. Спрессовывались навески массой М ₁ = 150 г и М ₂ = 300 г. Насыпная гравиметрическая плотность песка составила 1, 6 г/см³, шамотной крошки – 1, 17 г/см³. Гравиметрическая плотность беспористых песка и шамота принималась равной 2, 62 и 2, 92 г/см³ соответственно. Тогда относительная насыпная плотность песка составляет r ₀ = 0, 61; шамотной крошки – r ₀ = 0, 41.

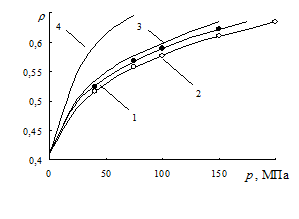
Экспериментальные данные по уплотняемости песка и шамотной крошки с разной массой навесок представлены на рис. 3.10. При оценке истинного осевого давления р_z для фиксированной плотности по кривым q ₁(r) и q ₂(r) определяли пару значений q ₁, q ₂ (на рис. 3.10, а показано линиями); затем по уравнению (3.81) рассчитывали величину р_z. Максимальная величина полного давления прессования в эксперименте составляла q _max = 200 МПа. При этом песок уплотняется до относительной плотности r = 0, 78; шамотная крошка – до r =0, 65. Сопротивление деформации при более высокой плотности находили экстраполированием по уравнению прессования р_z (r). Анализ показал, что среди известных уравнений прессования [5, 55, 71, 151] экспериментальные данные по уплотнению песка и шамотной крошки с хрупкой твердой фазой наиболее точно аппроксимируются уравнением прессования В.Е. Верниковского для огнеупорной керамики [71]

, (3.82)

где А, n – эмпирические константы. Эмпирическая зависимость между радиальным р_r и осевым р_z давлением принималась в следующем виде:

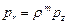. (3.83)

а

б

Р и с. 3.10. Зависимости между относительной плотностью r песка (а) и шамотной крошки (б) и силовыми параметрами прессования: 1 – q 1; 2 – q 2; 3 – рz; 4 – рr

Значения эмпирических констант А, n и m в уравнениях (3.82), (3.83) для исследованных материалов приведены в табл. 3.1.

Гидростатическое давление р = - s и интенсивность касательных напряжений Т при осесимметричном прессовании в закрытой матрице рассчитывали по зависимостям

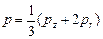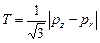; . (3.84)

Т а б л и ц а 3.1