Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Со смешанными граничными условиями

Краевая задача пластического деформирования при СВС-прессовании состоит в следующем. Горячая пористая нелинейно-вязкая заготовка, имеющая форму круглой пластины, помещена в оболочку из сыпучего материала и в жесткую закрытую цилиндрическую матрицу. Заданы температура и начальная относительная плотность заготовки и оболочки. Заготовку вместе с оболочкой сжимают жестким пуансоном, который перемещается с заданной скоростью v ₀ и развивает максимальное усилие прессования q. Скорость v ₀ мала, и поле напряжений удовлетворяет условию квазистатичности. Реологические свойства материала заготовки и оболочки известны. На границе оболочки с инструментом действуют силы трения. Скольжение оболочки относительно заготовки происходит без трения. Требуется определить конечные размеры и распределение плотности в материале заготовки при усилии прессования q.

Для описания процесса деформирования используется континуальная теория пластического течения сжимаемых сред. Решение сформулированной задачи состоит в нахождении в каждый момент времени t вектора скоростей v (x, t) и плотности r (x, t) точек деформируемой среды, положение которых в пространстве определяется радиусом-вектором x. При осесимметричном деформировании положение точек однозначно определяется двумя цилиндрическими координатами: r и z; поле скоростей – двумя компонентами вектора v: осевой скоростью v_z (r, z, t) и радиальной скоростью v_r (r, z, t). В связи с осевой симметрией рассматривается только меридиональное сечение (рис. 4.4).

Математическая постановка задачи включает:

1) кинематические соотношения Коши

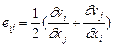; (4.18)

2) уравнение неразрывности

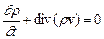; (4.19)

3) уравнения равновесия

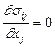; (4.20)

4) определяющие соотношения между тензором напряжений s_ij и тензором скоростей деформаций e_ij для пористой нелинейно-вязкой заготовки

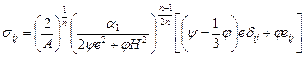(4.21)

и для сыпучей оболочки

. (4.22)

Параметры a ₁ в (4.21) и a ₂ в (4.22) принимаются равными

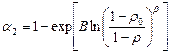, (4.23)

где r ₀ – насыпная плотность. В отличие от несжимаемых тел в определяющие уравнения уплотняемых тел в качестве структурного параметра входит плотность, изменение которой регулируется уравнением неразрывности.

Уравнения (4.18) - (4.23) образуют замкнутую систему уравнений с тремя неизвестными: плотностью r (x, t) и двумя компонентами поля скоростей v (x, t): v_z (r, z, t) и v_r (r, z, t). Система уравнений (4.18) - (4.23) дополняется начальными и граничными условиями.

Начальные условия задают начальное распределение плотности в заготовке 1 и оболочке 2. Принималось, что в начальный момент времени относительная плотность по объему заготовки и оболочки распределена однородно:

r ₁(x, 0) = r ₁₀; r ₂(x, 0) = r ₂₀. (4.24)

Рассмотрим граничные условия. Кинематические граничные условия отражают условие непроницаемости на внешней границе оболочки (см. рис. 4.1):

v_r (0, z, t) = 0; v_z (r, 0, t) = 0; v_z (r, h, t) = - v ₀; v_r (R _М, z, t) = 0. (4.25)

На границе «заготовка-оболочка» условие полного сцепления представляет собой равенство скоростей на всей поверхности контакта: v _{к 1}(x, t) = v _{к 2}(x, t). В отсутствие сил трения условие контактного взаимодействия на границе заготовки и оболочки представляет собой равенство нормальных компонент скоростей на всей поверхности контакта:

v_{n 1}(x, t) = v_{n 2}(x, t). (4.26)

На внешней границе оболочки при наличии трения имеют место смешанные граничные условия. Кинематическая часть граничных условий представляет собой условие непроницаемости:

v_r (r ₂, z, t) = 0; v_z (r, 0, t) = 0; v_z (r, h, t) = - v ₀; v_r (R ₂, z, t) = 0. (4.27)

Статическая часть граничных условий выражается законом трения на контактной поверхности через соотношение между нормальной s _n и касательной t составляющими вектора поверхностных напряжений. При малых нормальных давлениях действует закон трения Кулона: удельная сила трения скольжения t _ск пропорциональна нормальному давлению s_n: , где f _тр – коэффициент трения. С увеличением плотности коэффициент трения Кулона возрастает и зависимость f _тр(r) имеет вид (3.91): .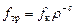

Величина t_ск не может превышать максимального значения t _max, допускаемого условием текучести. Следуя работе [44], положим, что t _max равно пределу текучести дисперсной среды на чистый сдвиг:
t _max = t _сд (закон трения Прандтля). Тогда при скольжении песчаной оболочки по внутренней поверхности инструмента будем иметь

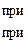
(4.28)

Удельная сила трения t _сд принимается пропорциональной площади живого сечения [44]. В рамках используемой реологической модели (4.15) живое сечение порошкового тела численно равно относительной доле контактного объема a ₂. Тогда напряжение t _сд будет равно t _сд = a ₂× t_S, где t_S – максимальный предел текучести на сдвиг дисперсной среды. При чистом сдвиге s = 0, и из определяющих соотношений (4.22) следует 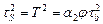. С учетом выражения для функции плотности j получим величину удельной силы трения t _сд:

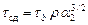. (4.29)

Для решения поставленной краевой задачи пластического деформирования со смешанными граничными условиями в работах [207, 211, 212, 240] использовался энергетический метод верхней оценки. Деформируемый объем разбивался на отдельные блоки – заготовка и три характерных блока песчаной оболочки. Кинематически допустимое поле скоростей задавалось из условия однородности скорости объемной деформации в пределах каждого блока. В модели учитывалось внешнее трение оболочки по закону Прандтля. Было получено хорошее соответствие расчетных и экспериментальных данных по кинетике изменения высоты средней части заготовки для трех СВС-композиций системы TiC-Ni.

Возможности энергетического метода позволяют рассчитать среднюю плотность и пропорциональное изменение геометрических размеров без искажения формы СВС-прессованной заготовки. В реальном процессе неоднородное распределение температуры и реологических свойств по объему заготовки приводит к существенному искажению ее формы [164]. Кроме того, различие реологических свойств продуктов синтеза и оболочки также обуславливает неоднородность напряженно-деформированного состояния при СВС-прессовании. Соответственно для описания закономерностей неоднородного деформирования необходимо использовать численные методы. Численное решение краевой задачи пластического деформирования при СВС-прессовании методом конечных элементов получено в работах [162, 210], ставших основанием дальнейшего изложения материала.