Трения материалов оболочки

а

б

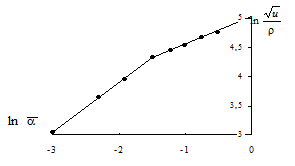
Р и с. 3.11. Линеаризация условия пластичности (3.64) при определении феноменологических параметров песка

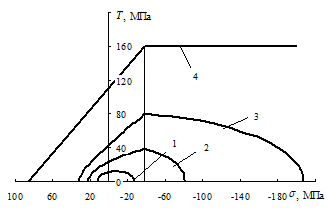
На рис. 3.12 на плоскости s – Т изображены кривые нагружения песка для различных значений относительной плотности r. Эти кривые наглядно иллюстрируют зависимость пластических свойств песка от его структурного состояния, величины и знака гидростатического давления. При гидростатическом напряжении кривые нагружения в зависимости от величины относительной плотности и знака функции F (3.67) представляют собой эллипс (r = 0, 63 < r _F), параболу (r = 0, 724 = r_F), гиперболу (r = 0, 83 > r_F) и прямую линию Кулона для беспористого состояния (r = 1). При напряжении независимо от величины относительной плотности r кривая нагружения является эллипсом, который в пределе при r = 1 вырождается в прямую Мизеса.

Форма кривых нагружения позволяет качественно оценить характер изменения плотности при пластическом течении песка. Согласно ассоциированному закону течения вектор скорости пластической деформации направлен по внешней нормали к кривой нагружения, а знак его проекции на гидростатическую ось s определяет знак скорости объемной деформации е. На кривой нагружения, обращенной выпуклостью в сторону отрицательных значений s, скорость объемной деформации е < 0 и пластическая деформация сопровождается уплотнением песка. Положительной скорости объемной деформации и разрыхлению соответствует кривая нагружения, которая выпуклостью обращена в сторону положительных значений s. Согласно данным рис. 3.12 уплотнение песка происходит только на эллиптических кривых нагружения. Пластическая деформация с разрыхлением песка имеет место на параболе, гиперболе и левой половине эллипса при напряжении . Отметим, что эффект трансформации формы поверхностей нагружения в зависимости от плотности порошковых материалов установлен экспериментально в работе [226].

Форма и положение кривых нагружения песка позволяют сделать два важных вывода. Во-первых, чистый сдвиг (s = 0) при любой степени уплотнения сопровождается разрыхлением песка или отрицательной дилатансией. Во-вторых, асимметричное положение кривых нагружения относительно оси Т предсказывает разносопротивляемость песка гидростатическому растяжению и сжатию. Таким образом, приведенные на рис. 3.12 данные наглядно иллюстрируют, что условие пластичности (3.64) описывает две основные особенности механического поведения порошковых материалов – пластическую дилатансию и деформационную анизотропию при гидростатическом нагружении.

В условии пластичности (3.64) через параметр a учитываются несвязанное начальное состояние и дискретно-контактная природа пластической деформации порошкового тела. Отмеченные свойства характерны и для условия пластичности с поверхностью нагружения четвертого порядка [60, 194], рассмотренного в разд. 1. Однако в связи с формально-математическим подходом это условие пластичности содержит такие феноменологические параметры, как пределы сопротивления растяжению, сжатию и кручению, которые технически сложно определить для порошковых тел. Условие пластичности (3.64) вытекает из физической, в частности энергетической, модели предельного состояния. Соответственно при определении феноменологических параметров используется более простая схема механических испытаний.

Р и с. 3.12. Кривые нагружения песка: 1 – r = 0, 63; 2 – r = 0, 724; 3 – r = 0, 83; 4 – r = 1

На основании полученных экспериментальных данных построим частное условие пластичности для процесса уплотнения порошкового материала в замкнутом объеме. По форме частное условие пластичности аналогично условиям пластичности (3.59), (3.64, б) и через полную энергию упругой деформации порошкового тела u может быть записано следующим образом:

. (3.87)

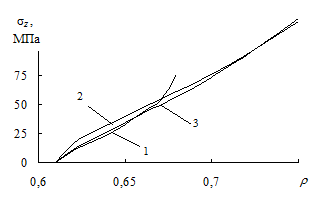
В общем условии пластичности (3.64, б) феноменологические параметры b и t ₀ определены для напряжений , поэтому прямая экстраполяция условия пластичности (3.64, б) в область значений (рис. 3.13, кривая 2) дает завышенные значения расчетных напряжений по сравнению с условием пластичности (3.64, а) – кривая 1 на рис. 3.13. Уменьшить это расхождение можно, если феноменологические параметры в частном условии пластичности определить независимо от величины средних напряжений s.

Р и с. 3.13. Расчетные осевые напряжения s z при прессовании песка в закрытой матрице: 1 – расчет по (3.64, а); 2 – расчет по (3.64, б); 3 – расчет по упрощенной модели

Эффективное сопротивление сдвигу t ₀ твердой фазы, найденное из общего условия пластичности, будем использовать и в частном условии пластичности. Тогда задача построения частного условия пластичности сводится к аппроксимации экспериментальной зависимости u (r) функцией 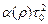во всем диапазоне напряжений s.

На рис. 3.14 представлены экспериментальные зависимости u (r) для песка и шамотной крошки. Следует отметить, что для эллиптических условий пластичности, в которых рассматривается предельное состояние всей твердой фазы, параметр a в соотношении (3.87) равен относительной плотности: a = r. В этом случае зависимость u (r) является линейной, и при насыпной плотности энергия упругого деформирования имеет конечное значение 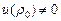. Экспериментальные данные (см. рис. 3.14) подтверждают несостоятельность такой каркасной модели порошкового тела. Это касается как нелинейного характера самой зависимости u (r), так и величины упругой энергии предельного состояния при насыпной плотности, когда 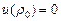. Нелинейный характер экспериментальной кривой u (r) указывает на то, что в порошковом материале в предельном упругом состоянии находится не весь объем твердой фазы, а лишь его часть.

В частном условии пластичности зависимость a (r) выполняет роль функции, которая с точностью до постоянного множителя аппроксимирует экспериментальную зависимость u (r). Однопараметрические зависимости М.Ю. Бальшина (3.47) и Г.Е. Ждановича (3.48) неудовлетворительно описывают экспериментальные данные. Хорошую аппроксимацию обеспечивает двухпараметрическая функция, которая построена на основании уравнения прессования В.Е. Верниковского (3.82):

, (3.88)

где B, b – эмпирические константы.

u × 10-3 а

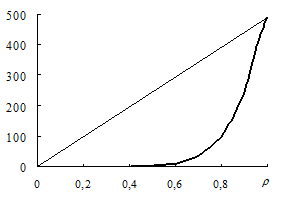
u × 10-3 б

Р и с. 3.14. Изменение удельной упругой энергии u (r) при уплотнении песка (а) и шамотной крошки (б)

Количественная оценка параметров В и b проводилась методом наименьших квадратов при минимизации функционала

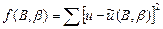, (3.89)

где 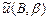– предельная энергия упругого деформирования при частном условии пластичности. Функционал (3.89) минимизировали методом Дэвидона-Флетчера-Пауэла [25, 103]. Для песка получены следующие значения эмпирических констант: В = 0, 71; b = 1, 45. При этих значениях расчетные напряжения для упрощенной модели отличаются от расчетных напряжений общей модели не более, чем на 5% (см. рис. 3.13). Эмпирические константы B и b для шамотной крошки и песчано-шамотной смеси приведены в табл. 3.2.

Экспериментальная зависимость u (r) описывает предельное состояние порошкового тела для любых значений гидростатического напряжений и обоих механизмов деформации. Соответственно такими же свойствами характеризуется условие пластичности, у которого материальные константы определены из зависимости u (r).

Для построения математической модели СВС-прессования с реальными граничными условиями необходима информация о триботехнических характеристиках материала оболочки и, в частности, коэффициенте трения Кулона f _тр. Коэффициент трения Кулона f _тр уплотняемого материала и инструмента находили из соотношения [132]

, (3.90)

где R – радиус матрицы; d – гравиметрическая плотность прессовки. Обработка экспериментальных данных (см. рис. 3.10) по соотношению (3.90) показала, что коэффициент f _тр убывает с увеличением плотности материала по закону

f _тр = f _к× r ^{- с} , (3.91)

где f _к, с – эмпирические константы. Множитель f _к в выражении (3.91) представляет собой коэффициент трения беспористого материала. Для песка получено f _к = 0, 63, что хорошо согласуется с коэффициентом сцепления колес с рельсами, посыпанными песком: f _тр = 0, 6 [87]. Песок при этом находится в раздробленном состоянии, которое близко к беспористому состоянию. Сводные данные о параметрах внешнего трения исследованных материалов представлены
в табл. 3.2.

Заканчивая изложение материала данного раздела, сформулируем основные полученные результаты и выводы.

1. Для разработанной реологической модели пористого вязкого тела с жидкой фазой показано, что в рамках модели со свободной поверхностью и приближения идеальной жидкостью жидкая фаза может рассматриваться как элемент поровой структуры и возможно простое суммирование объемной концентрации расплава и пор. Реологические свойства пористого твердожидкого материала в этом случае определяются только объемной долей и сдвиговой вязкостью твердой фазы. Корректность предложенной реологической модели показана на примере решения обратной задачи реологии при горячем прессовании порошка твердого сплава ВК6.

2. Выполнено теоретическое обоснование структурной модели порошковых материалов, учитывающей контактную природу неупругого деформирования частиц порошка. Модель представляет собой хаотично ориентированную контактно-стержневую систему, которая состоит из цилиндров, контактирующих своими основаниями, и испытывает однородную деформацию растяжения-сжатия. Методом диссипативной функции получены определяющие соотношения для порошковых материалов с различной реологией твердой фазы. В эти соотношения входит новый феноменологический параметр – объемная доля контактного объема частиц порошка. Предложенная контактно-стержневая модель удовлетворяет граничным условиям для начального состояния насыпной плотности и показывает хорошее соответствие с экспериментальными данными по изостатическому прессованию металлических порошков.

3. На основании контактно-стержневой модели и гипотезы Бельтрами сформулировано общее условие пластичности, учитывающее двойственный механизм пластической деформации порошковых материалов – межчастичное скольжение (структурная деформация) и пластическую деформацию (или разрушение) частиц. Границей между структурным и пластическим деформированием служит величина гидростатического напряжения s ^*, при которой наступает пластический сдвиг или разрушение гипотетического беспористого тела Кулона. Показано, что форма поверхности нагружения и определяющие соотношения функционально связаны со структурным состоянием через плотность материала и напряженным состоянием через гидростатическое напряжение s ^*. Это усложняет практическое применение общего условия пластичности. Для описания процесса уплотнения в замкнутом объеме с монотонным нагружением построено частное условие пластичности, которое посредством аппроксимации экспериментальной зависимости изменения полной энергии упругой деформации интегрально учитывает структурную и пластическую деформацию порошкового материала.

4. На основании проведенных экспериментальных исследований определены феноменологические параметры для общего и частного условий пластичности сыпучих материалов теплоизолирующей оболочки – песка, шамотной крошки и песчано-шамотной смеси. Для общего условия пластичности построены кривые нагружения песка от его сыпучего состояния до условно - беспористого состояния. Вид кривых нагружения подтвердил, что предложенное условие пластичности описывает две основные особенности механического поведения порошковых материалов – пластическую дилатансию и деформационную анизотропию при гидростатическом нагружении.

5. По результатам экспериментальных исследований определены триботехнические характеристики песка, шамотной крошки и песчано-шамотной смеси, необходимые для решения краевой задачи пластического деформирования со смешанными граничными условиями.